Bài 1, 2, 3 trang 122 SGK Toán 4

Bài 1: So sánh hai phân số.

Lựa chọn câu để xem lời giải nhanh hơn

Bài 1

Video hướng dẫn giải

So sánh hai phân số:

a) \( \displaystyle \displaystyle{3 \over 4}\) và \( \displaystyle \displaystyle{4 \over 5}\) b) \( \displaystyle \displaystyle{5 \over 6}\) và \( \displaystyle \displaystyle{7 \over 8}\) c) \( \displaystyle \displaystyle{2 \over 5}\) và \( \displaystyle \displaystyle{3 \over 10}\).

Phương pháp giải:

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

Lời giải chi tiết:

a) Quy đồng mẫu số hai phân số \( \displaystyle{3 \over 4}\) và \( \displaystyle{4 \over 5}\) :

\( \displaystyle{3 \over 4} = {{3 \times 5} \over {4 \times 5}} = {{15} \over {20}};\quad \)\( \displaystyle{4 \over 5} = {{4 \times 4} \over {5 \times 4}} = {{16} \over {20}}\)

Vì \( \displaystyle{{15} \over {20}} < {{16} \over {20}}\) nên \( \displaystyle{3 \over 4}< \displaystyle{4 \over 5}\).

b) Quy đồng mẫu số hai phân số \( \displaystyle{5 \over 6}\) và \( \displaystyle{7 \over 8}\):

\( \displaystyle{5 \over 6} = {{5 \times 8} \over {6 \times 8}} = {{40} \over {48}}; \quad \)\( \displaystyle{7 \over 8} = {{7 \times 6} \over {8 \times 6}} = {{42} \over {48}}\)

Vì \( \displaystyle{{40} \over {48}} < {{42} \over {48}}\) nên \( \displaystyle{5 \over 6} < \displaystyle{7 \over 8}\).

c) Quy đồng mẫu số phân số \( \displaystyle{2 \over 5}\) và giữ nguyên phân số \( \displaystyle{3 \over 10}\):

\( \displaystyle{2 \over 5} = {{2 \times 2} \over {5 \times 2}} = {4 \over {10}}\)

Vì \( \displaystyle{4 \over {10}} > {3 \over {10}}\) nên \( \displaystyle{2 \over 5} > \displaystyle{3 \over 10}\).

Bài 2

Video hướng dẫn giải

Rút gọn rồi so sánh hai phân số :

\( \displaystyle \displaystyle{6 \over {10}}\) và \( \displaystyle \displaystyle{4 \over 5}\) b) \( \displaystyle \displaystyle{3 \over 4}\) và \( \displaystyle \displaystyle{6 \over {12}}\)

Phương pháp giải:

- Rút gọn các phân số đã cho thành phân số tối giản (nếu được).

- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

Lời giải chi tiết:

a) Rút gọn phân số \( \displaystyle{6 \over {10}}\) và giữ nguyên phân số \( \displaystyle{4 \over 5}\):

\( \displaystyle{6 \over {10}} = {{6:2} \over {10:2}} = {3 \over 5}\)

Vì \( \displaystyle{3 \over 5}<{4 \over 5}\) nên \( \displaystyle{6 \over {10}} < \displaystyle{4 \over 5}\) .

b) Rút gọn phân số \( \displaystyle{6 \over {12}}\) và giữ nguyên phân số \( \displaystyle{3 \over 4}\) :

\( \displaystyle{6 \over {12}} = {{6:3} \over {12:3}} = {2 \over 4}\)

Vì \( \displaystyle{3 \over 4} > \displaystyle{2 \over 4}\) nên \( \displaystyle{3 \over 4} > \displaystyle{6 \over {12}}\).

Bài 3

Video hướng dẫn giải

Mai ăn \( \displaystyle \displaystyle{3 \over 8}\) cái bánh, Hoa ăn \( \displaystyle \displaystyle{2 \over 5}\) cái bánh. Ai ăn nhiều bánh hơn ?

Phương pháp giải:

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

Lời giải chi tiết:

Quy đồng mẫu số hai phân số :

\( \displaystyle\eqalign{
& {3 \over 8} = {{3 \times 5} \over {8 \times 5}} = {{15} \over {40}} ; \cr
& {2 \over 5} = {{2 \times 8} \over {5 \times 8}} = {{16} \over {40}} .\cr} \)

Vì \( \displaystyle{{16} \over {40}} > {{15} \over {40}}\) nên \(\dfrac{2}{5} > \dfrac{3}{8}\).

Vậy Hoa là người ăn nhiều bánh hơn.

Lý thuyết

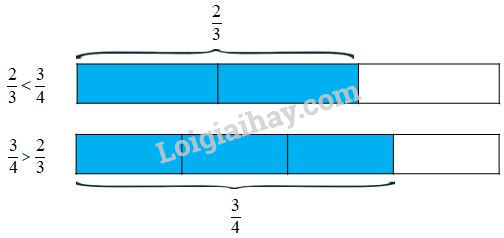
Ví dụ : So sánh hai phân số \(\dfrac{2}{3}\) và \(\dfrac{3}{4}\).

a) Lấy hai băng giấy bằng nhau. Chia băng giấy thứ nhất thành \(3\) phần bằng nhau, lấy \(2\) phần, tức là lấy \(\dfrac{2}{3}\) băng giấy. Chia băng giấy thứ hai thành \(4\) phần bằng nhau, lấy \(3\) phần, tức là lấy \(\dfrac{3}{4}\) băng giấy.

Nhìn hình vẽ ta thấy :