 Giải toán 4, giải bài tập toán 4, để học tốt Toán 4 đầy đủ số học và hình học
Giải toán 4, giải bài tập toán 4, để học tốt Toán 4 đầy đủ số học và hình học
 CHƯƠNG IV. PHÂN SỐ - CÁC PHÉP TÍNH VỚI PHÂN SỐ. GIỚI TH..
CHƯƠNG IV. PHÂN SỐ - CÁC PHÉP TÍNH VỚI PHÂN SỐ. GIỚI TH.. Bài 1, 2, 3 trang 112 SGK Toán 4
Bài 1: Viết số thích hợp vào ô trống.
Bài 1
Video hướng dẫn giải
Viết số thích hợp vào ô trống:
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
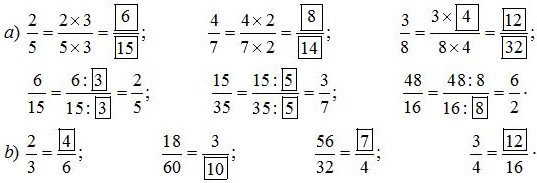
Bài 2
Video hướng dẫn giải
Tính rồi so sánh kết quả:
a) 18 : 3 và (18 × 4 ) : (3 × 4); b) 81 : 9 và (81 : 3) : (9 : 3)
Nhận xét:
Nếu nhân (hoặc chia) số bị chia và số chia với cùng một số tự nhiên khác 0 thì giá trị của thương không đổi.
Phương pháp giải:
Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.
Lời giải chi tiết:
a) 18 : 3 = 6 ;
(18 × 4 ) : (3 × 4) = 72 : 12 = 6
Vậy kết quả của 18 : 3 và (18 × 4 ) : (3 × 4) bằng nhau.
b) 81 : 9 = 9 ;
(81 : 3) : (9 : 3) = 27 : 3 = 9
Vậy kết quả 81 : 9 và ( 81 : 3) : (9 : 3) bằng nhau.
Bài 3
Video hướng dẫn giải
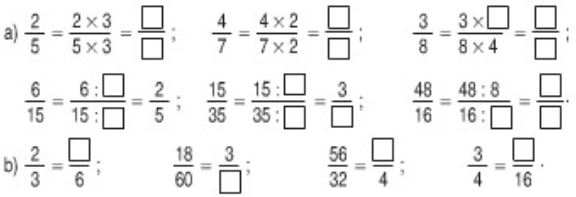
Viết số thích hợp vào ô trống :
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
Cách giải:
Ta có:
\(\dfrac{50}{75} = \dfrac{50:5}{75:5} =\dfrac{10}{15} \); \(\dfrac{10}{15} = \dfrac{10:5}{15:5} =\dfrac{2}{3} \);
\(\dfrac{3}{5} = \dfrac{3\times2}{5\times2} =\dfrac{6}{10} \); \(\dfrac{3}{5} = \dfrac{3\times3}{5\times3} =\dfrac{9}{15} \);
\(\dfrac{3}{5} = \dfrac{3\times4}{5\times4} =\dfrac{12}{20} \).
Vậy ta có kết quả như sau :

Lý thuyết
1. Phân số bằng nhau
a) Có hai băng giấy bằng nhau.

b) Nhận xét: $\dfrac{3}{4} = \dfrac{{3 \times 2}}{{4 \times 2}} = \dfrac{6}{8}$ và \(\dfrac{6}{8} = \dfrac{{6:2}}{{8:2}} = \dfrac{3}{4}\).
Từ nhận xét này , có thể nêu tính chất cơ bản của phân số như sau:
Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.
Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác \(0\) thì sau khi chia ta được một phân số bằng phân số đã cho.












Danh sách bình luận