 Giải toán 4, giải bài tập toán 4, để học tốt Toán 4 đầy đủ số học và hình học
Giải toán 4, giải bài tập toán 4, để học tốt Toán 4 đầy đủ số học và hình học
 CHƯƠNG IV. PHÂN SỐ - CÁC PHÉP TÍNH VỚI PHÂN SỐ. GIỚI TH..
CHƯƠNG IV. PHÂN SỐ - CÁC PHÉP TÍNH VỚI PHÂN SỐ. GIỚI TH.. Bài 1, 2, 3, 4 trang 137 SGK Toán 4
Bài 1. Tính rồi rút gọn:...
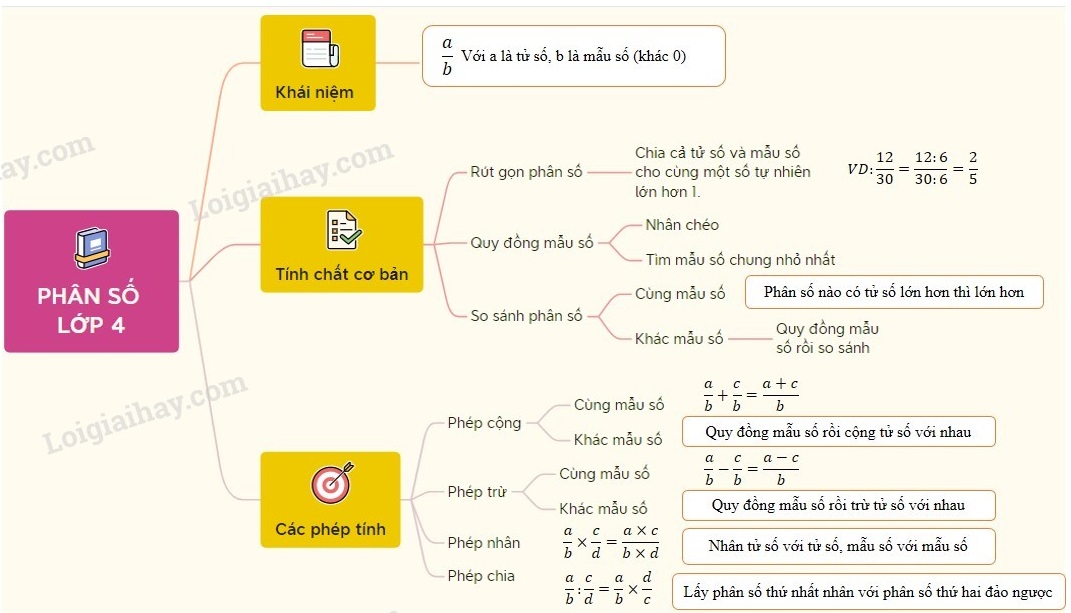
Sơ đồ tư duy: Phân số lớp 4
Bài 1
Video hướng dẫn giải
Tính rồi rút gọn:
a) \(\displaystyle {2 \over 7}:{4 \over 5};\) b) \( \displaystyle {3 \over 8}:{9 \over 4};\)
c) \(\displaystyle {8 \over {21}}:{4 \over 7};\) d) \(\displaystyle {5 \over 8}:{{15} \over 8}\)
Phương pháp giải:
Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
a) \( \displaystyle{2 \over 7}:{4 \over 5} = {2 \over 7} \times {5 \over 4} = {{10} \over {28}} = {{10:2} \over {28:2}} \)\( \displaystyle= {5 \over {14}};\)
Hoặc : \( \displaystyle{2 \over 7}:{4 \over 5} = {2 \over 7} \times {5 \over 4} = {{2 \times 5 } \over {7 \times 4 }} \)\( \displaystyle= {{2\times 5} \over {7 \times 2 \times 2}} = {5 \over {14}};\)
b) \( \displaystyle{3 \over 8}:{9 \over 4} = {3 \over 8} \times {4 \over 9} = {{12} \over {72}} = {{12:12} \over {72:12}}\)\( \displaystyle = {1 \over 6};\)
Hoặc : \( \displaystyle{3 \over 8}:{9 \over 4} = {3 \over 8} \times {4 \over 9} = {{3\times 4 } \over {8 \times 9}} \)\( \displaystyle = {{3 \times 4} \over {4 \times 2 \times 3 \times 3}} = {1 \over 6};\)
c) \( \displaystyle{8 \over {21}}:{4 \over 7} = {8 \over {21}} \times {7 \over 4} = {{56} \over {84}} \) \(\displaystyle= {{56:28} \over {84:28}} = {2 \over 3};\)
Hoặc : \( \displaystyle{8 \over {21}}:{4 \over 7} = {8 \over {21}} \times {7 \over 4} = {{8\times 7} \over {21 \times 4}} \) \(\displaystyle= {{2 \times 4 \times 7} \over {3 \times 7 \times 4}} = {2 \over 3};\)
d) \( \displaystyle{5 \over 8}:{{15} \over 8} = {5 \over 8} \times {8 \over {15}} = {{40} \over {120}} \) \(\displaystyle = {{40:40} \over {120:40}} = {1 \over 3}.\)
Hoặc : \( \displaystyle{5 \over 8}:{{15} \over 8} = {5 \over 8} \times {8 \over {15}} = {{5 \times 8} \over {8 \times 15}} \) \(\displaystyle = {{5 \times 8} \over {8 \times 5 \times 3}} = {1 \over 3}.\)
Bài 2
Video hướng dẫn giải
Tính (theo mẫu):
Mẫu: \( \displaystyle 2:{3 \over 4} = {2 \over 1} : { 3 \over 4} = { 2\over 1} \times {4 \over 3 }= {8 \over 3}\)
Ta có thể viết gọn như sau: \( \displaystyle 2:{3 \over 4} = {{2 \times 4} \over 3} = {{8} \over 3}\)
a) \( \displaystyle3:{5 \over 7};\) b) \( \displaystyle4:{1 \over 3};\) c) \( \displaystyle5:{1 \over 6}.\)
Phương pháp giải:
Để chia số tự nhiên cho phân số ta có thể viết số tự nhiên dưới dạng phân số có mẫu số là \(1\), sau đó thực hiện phép chia hai phân số như thông thường; hoặc ta viết gọn lại tương tự như ở ví dụ mẫu.
Lời giải chi tiết:
\( \displaystyle\eqalign{
& a)\,\,3:{5 \over 7} = {{3 \times 7} \over 5} = {{21} \over 5}; \cr
& b)\,\,4:{1 \over 3} = {{4 \times 3} \over 1} = 12; \cr
& c)\,\,5:{1 \over 6} = {{5 \times 6} \over 1} = 30. \cr} \)
Bài 3
Video hướng dẫn giải
Tính bằng hai cách:
\( \displaystyle a)\,\,\left( {{1 \over 3} + {1 \over 5}} \right) \times {1 \over 2}; \) \( \displaystyle b)\,\,\left( {{1 \over 3} - {1 \over 5}} \right) \times {1 \over 2}. \)
Phương pháp giải:
Cách 1: biểu thức có dấu ngoặc thì ta tính trong ngoặc trước, ngoài ngoặc sau.
Cách 2: Áp dụng công thức nhân một tổng hoặc một hiệu với một số:
\((a+b)\times c = a \times c + b \times c\) ; \((a-b)\times c = a \times c - b \times c\)
Lời giải chi tiết:
a) Cách 1:
\( \displaystyle\,\,\left( {{1 \over 3} + {1 \over 5}} \right) \times {1 \over 2} = \left( {{5 \over {15}} + {3 \over {15}}} \right) \times {1 \over 2} \)
\( \displaystyle= {8 \over {15}} \times {1 \over 2} = {8 \over {30}}= {4 \over {15}};\)
Cách 2:
\( \displaystyle\,\,\left( {{1 \over 3} + {1 \over 5}} \right) \times {1 \over 2} = {1 \over 3} \times {1 \over 2} + {1 \over 5} \times {1 \over 2} \)
\( \displaystyle= {1 \over 6} + {1 \over {10}} = {{10} \over {60}} + {6 \over {60}} = {{16} \over {60}} = {4 \over {15}}\)
b) Cách 1:
\( \displaystyle\,\left( {{1 \over 3} - {1 \over 5}} \right) \times {1 \over 2} = \left( {{5 \over {15}} - {3 \over {15}}} \right) \times {1 \over 2} \)
\( \displaystyle= {2 \over {15}} \times {1 \over 2} = {2 \over {30}}= {1 \over {15}}\)
Cách 2:
\( \displaystyle\left( {{1 \over 3} - {1 \over 5}} \right) \times {1 \over 2} = {1 \over 3} \times {1 \over 2} - {1 \over 5} \times {1 \over 2}\)
\( \displaystyle= {1 \over 6} - {1 \over {10}}\)\( \displaystyle= {{10} \over {60}} - {6 \over {60}}\)\( \displaystyle= {4 \over {60}} = {1 \over {15}}\)
Bài 4
Video hướng dẫn giải
Cho các phân số \( \displaystyle{1 \over 2}\,;\;{1 \over 3}\,;\;{1 \over 4}\,;\;{1 \over 6}\). Hỏi mỗi phân số đó gấp mấy lần \( \displaystyle{1 \over {12}}\)?
Mẫu: \( \displaystyle{1 \over 2}:{1 \over {12}} = {1 \over 2} \times {{12} \over 1} = {{12} \over 2} = 6\)
Vậy: \( \displaystyle{1 \over 2}\) gấp 6 lần \( \displaystyle{1 \over {12}}\).
Phương pháp giải:
Thực hiện phép chia hai phân số để tìm thương của hai phân số đó.
Lời giải chi tiết:
+) \( \displaystyle{1 \over 3}:{1 \over {12}} = {1 \over 3} \times {{12} \over 1} = {{12} \over 3} = 4\)
Vậy: \( \displaystyle{1 \over 3}\) gấp \(4\) lần \( \displaystyle{1 \over {12}}\).
+) \( \displaystyle{1 \over 4}:{1 \over {12}} = {1 \over 4} \times {{12} \over 1} = {{12} \over 4} = 3\)
Vậy: \( \displaystyle{1 \over 4}\) gấp \(3\) lần \( \displaystyle{1 \over {12}} \).
+) \( \displaystyle{1 \over 6}:{1 \over {12}} = {1 \over 6} \times {{12} \over 1} = {{12} \over 6} = 2\)
Vậy: \( \displaystyle{1 \over 6}\) gấp \(2\) lần \( \displaystyle{1 \over {12}}\).
Loigiaihay.com











Danh sách bình luận