 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Bài 4. Đường trung bình của tam giác, của hình thang
Bài 4. Đường trung bình của tam giác, của hình thang
Lý thuyết đường trung bình của tam giác
Đường trung bình cuả tam giác là đoạn thằng nối trung điểm hai cạnh của tam giác.
1. Kiến thức cần nhớ
Đường trung bình của tam giác

Định lí 1:
Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Định lí 2:
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Ví dụ:
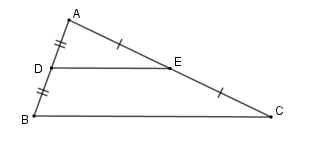
+ \(\Delta ABC\) có \(D\) là trung điểm của \(AB\) , \(E\) là trung điểm của \(AC\) nên \(DE\) là đường trung bình của tam giác \(ABC\) suy ra \(DE{\rm{//}}BC;\,DE = \dfrac{1}{2}BC.\)
+ Nếu \(\left\{ \begin{array}{l}DA = DB\\DE{\rm{//}}BC\end{array} \right.\) suy ra \(EC = EA\) .
2. Các dạng toán thường gặp
Dạng 1: Chứng minh các hệ thức về cạnh và góc. Tính các cạnh và góc
Phương pháp:
Sử dụng tính chất đường trung bình của tam giác
+ Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+ Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Dạng 2: Chứng minh một cạnh là đường trung bình của tam giác
Phương pháp:
Sử dụng định nghĩa đường trung bình của tam giác: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
3. Bài tập vận dụng
Câu 1. Chọn câu đúng.
A. Đường trung bình của tam giác là đường nối trung điểm ba cạnh của hình tam giác
B. Đường trung bình của tam giác của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
C. Trong một tam giác chỉ có một đường trung bình.
D. Đường trung bình của tam giác là đường nối từ một đỉnh đến trung điểm cạnh đối diện.
Lời giải: Đường trung bình của tam giác của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
Đáp án B
Câu 2. Cho tam giác ABC có E, F lần lượt là trung điểm của AB, BC. Phát biểu nào sau đây là đúng:
A. EF có độ dài bằng hai lần BC.
B. EF có độ dài bằng hai lần AB.
C. EF có độ dài bằng một nửa AC.
D. EF có độ dài bằng một nửa BC.
Lời giải:
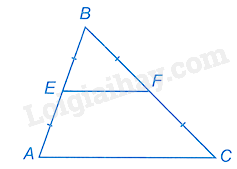
E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của tam giác ABC.
Suy ra EF có độ dài bằng một nửa của AC.
Đáp án C
Câu 3. Chọn câu đúng. Cho hình vẽ sau:
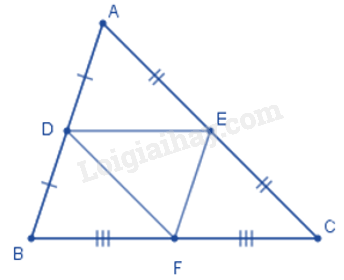
Đường trung bình của tam giác ABC là:
A. DE
B. DF
C. EF
D. Cả A, B, C đều đúng
Lời giải: Xét tam giác ABC có D, E, F lần lượt là trung điểm các cạnh AB, AC, BC nên DE, DF, EF là ba đường trung bình của tam giác ABC.
Đáp án D
Câu 4. Cho tam giác MNP có A, B theo thứ tự là trung điểm của NP, MN. Biết AB = 3dm. Khi đó:
A. MP = 6dm
B. MN = 5,5dm
C. NP = 4dm
D. MP = 1,5dm
Lời giải:
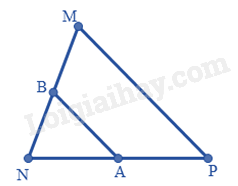
Xét tam giác MNP có:
A là trung điểm của NP
B là trung điểm của MN
Suy ra: \(AB = \frac{{MP}}{2} \), do đó \( MP = 2{\rm{A}}B = 2.3 = 6(dm)\)
Đáp án A
Câu 5. Cho tam giác ABC có BC = 6cm, các đường trung tuyến BE, CD. Khi đó độ dài cạnh DE là
A. 12cm
B. 6cm
C. 3cm
D. 2cm
Lời giải:
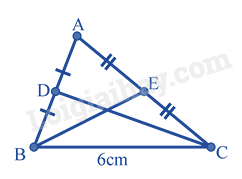
Vì BE là trung tuyến của tam giác ABC suy ra E là trung điểm của AC
Vì CD là trung tuyến của tam giác ABC suy ra D là trung điểm của AB
Xét tam giác ABC có DE là đường trung bình của tam giác ABC nên:
\(DE = \frac{1}{2}BC = \frac{1}{2}.6 = 3(cm)\)
Đáp án C
Câu 6. Cho tam giác ABC. Trên cạnh AB, AC lần lượt lấy các điểm E, F sao cho AE = BE, AF = FC. Khi đó \(\frac{{BC}}{{EF}}\) bằng:
A. 2
B. 1
C. \(\frac{1}{2}\)
D. 3
Lời giải:
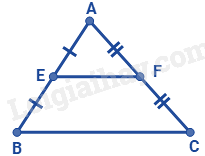
Vì AE = BE, AF = FC nên EF là đường trung bình của tam giác ABC.
Do đó: BC = 2.EF.
Vậy \(\frac{{BC}}{{EF}} = 2\).
Đáp án A
Câu 7. Cho tam giác ABC vuông tại A như hình vẽ dưới đây: Biết AB = 6cm; AC = 8 cm. Độ dài đường trung bình ứng với cạnh BC là
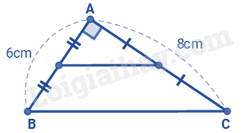
A. 10cm
B. 5cm
C. 20cm
D. 7cm
Lời giải: Xét tam giác ABC vuông tại A, áp dụng định lí Pytago, ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10cm\)
Vì đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy nên độ dài đường trung bình ứng với cạnh BC là: \(\frac{1}{2}.10 = 5cm\) .
Đáp án B
Câu 8. Cho tam giác ABC có chu vi bằng 32cm. Gọi E, F, P là trung điểm của các cạnh AB, BC, AC. Chu vi của tam giác PFE bằng:
A. 17cm
B. 33cm
C. 15cm
D. 16cm
Lời giải:
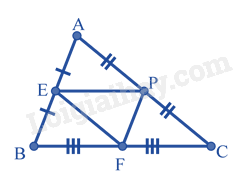
Vì E. F, P là trung điểm của các cạnh AB. BC, AC của tam giác ABC nên EP, PF, FE là đường trung bình của tam giác ABC.
Do đó \( EP = \frac{1}{2}BC;PF = \frac{1}{2}AB;F{\rm{E}} = \frac{1}{2}AC\)
Suy ra \(EP + PF + F{\rm{E}} = \frac{1}{2}\left( {BC + AB + AC} \right) = \frac{1}{2}.32 = 16cm\)
Đáp án D












Danh sách bình luận