Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 9. Hình chữ nhật

Bài 64 trang 100 SGK Toán 8 tập 1


Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D

Đề bài

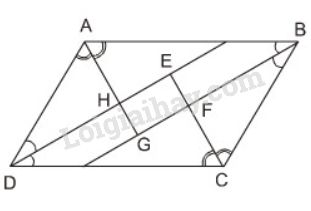
Cho hình bình hành \(ABCD\). Các tia phân giác của các góc \(A, B, C, D\) cắt nhau như trên hình \(91.\) Chứng minh rằng \(EFGH\) là hình chữ nhật. 

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Áp dụng:

+) Định lí: Tổng \(3\) góc của một tam giác bằng \(180^o\).

+) Dấu hiệu nhận biết hình chữ nhật: Tứ giác có ba góc vuông là hình chữ nhật.

Lời giải chi tiết

Theo giả thiết \(ABCD\) là hình bình hành nên \(AD//BC,AB//CD\) 

Vì \(AD//BC\) \( \Rightarrow \widehat {DAB} + \widehat {ABC}= {180^0}\) (hai góc trong cùng phía bù nhau)

Vì \(AG\) là tia phân giác \(\widehat {DAB}\) (giả thiết)

\( \Rightarrow \) \(\widehat {BAG}=\widehat {DAH} = \dfrac{1}{2}\widehat {DAB}\) (tính chất tia phân giác)

Vì \(BG\) là tia phân giác \(\widehat {ABC}\) (giả thiết)

\( \Rightarrow \)  \(\widehat {ABG} = \dfrac{1}{2}\widehat {ABC}\)

Do đó: \(\widehat {BAG} + \widehat {ABG} = \dfrac{1}{2}\left( {\widehat {DAB} + \widehat {ABC}} \right) \)\(= \dfrac{1}{2}{.180^0} = {90^0}\)

Xét \(\Delta AGB\) có:

\(\widehat {BAG} + \widehat {ABG} = {90^0}\)

Áp dụng định lí tổng ba góc trong một tam giác vào tam giác \(AGB\) ta có:

\(\widehat {BAG} + \widehat {ABG} + \widehat {AGB} = {180^0}\)

\( \Rightarrow\widehat {AGB} =180^0- (\widehat {BAG} + \widehat {ABG} )\)\(=180^0-{90^0}=90^0\) (*)

+ Vì \(AB//DC\) \( \Rightarrow \widehat {DAB} + \widehat {ADC}= {180^0}\) (hai góc trong cùng phía bù nhau)

+ Vì \(DE\) là tia phân giác \(\widehat {ADC}\) (giả thiết)

\( \Rightarrow \) \(\widehat {ADH}=\widehat {EDC} = \dfrac{1}{2}\widehat {ADC}\) (tính chất tia phân giác)

Do đó: \(\widehat {DAH} + \widehat {ADH} = \dfrac{1}{2}\left( {\widehat {DAB} + \widehat {ADC}} \right) \)\(= \dfrac{1}{2}{.180^0} = {90^0}\)

Áp dụng định lí tổng ba góc trong một tam giác vào tam giác \(ADH\) ta có:

\(\widehat {DAH} + \widehat {ADH} + \widehat {AHD} = {180^0}\)

\( \Rightarrow\widehat {AHD} =180^0- (\widehat {DAH} + \widehat {ADH} )\)\(=180^0-{90^0}=90^0\)

Suy ra \(AH\bot HD\) nên \(\widehat {EHG}=90^0\) (**)

Chứng minh tương tự:

Ta có: \( \widehat {DCB} + \widehat {ADC}= {180^0}\) (hai góc trong cùng phía bù nhau)

Mà \(\widehat{ECD}=\dfrac{1}2\widehat {DCB}\) (do CE là phân giác góc DCB)

Nên \(\widehat {EDC} + \widehat {ECD} = \dfrac{1}{2}\left( {\widehat {ADC} + \widehat {DCB}} \right) \)\(= \dfrac{1}{2}{.180^0} = {90^0}\)

Lại có: 

\(\widehat {EDC} + \widehat {ECD} + \widehat {DEC} = {180^0}\) (tổng ba góc trong tam giác DEC)

\( \Rightarrow\widehat {DEC} =180^0- (\widehat {EDC} + \widehat {ECD} )\)\(=180^0-{90^0}=90^0\)

Hay \(\widehat {HEF} = {90^0}\) (***)

Từ (*), (**) và (***) ta thấy tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

Loigiaihay.com


Bình chọn:
4.5 trên 278 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store