-
PHẦN ĐẠI SỐ - TOÁN 8 TẬP 1
-
CHƯƠNG I. PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3. Những hằng đẳng thức đáng nhớ
- Bài 4. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 5. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Ôn tập chương I: Phép nhân và phép chia các đa thức
- Đề kiểm tra 15 phút - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Đại số 8
-
CHƯƠNG II. PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Ôn tập chương II: Phân thức đại số
- Đề kiểm tra 15 phút – Chương 2 – Đại số 8
- Đề kiểm tra 45 phút (1 tiết ) – Chương 2 – Đại số 8
-
-
PHẦN HÌNH HỌC - TOÁN 8 TẬP 1
-
CHƯƠNG I. TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương I: Tứ giác
- Đề kiểm tra 15 phút - Chương 1 - Hình học 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 8
-
CHƯƠNG II. ĐA GIÁC, DIỆN TÍCH ĐA GIÁC
- Bài 1. Đa giác. Đa giác đều
- Bài 2. Diện tích hình chữ nhật
- Bài 3. Diện tích tam giác
- Bài 4. Diện tích hình thang
- Bài 5. Diện tích hình thoi
- Bài 6. Diện tích đa giác
- Ôn tập chương II: Đa giác. Diện tích đa giác
- Đề kiểm tra 15 phút - Chương 2 - Hình học 8
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 8
-
-
Đề cương ôn tập học kì 1 toán 8
-
Đề thi học kì 1 mới nhất có lời giải
-
PHẦN ĐẠI SỐ - TOÁN 8 TẬP 2
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
- Bài 1. Mở đầu về phương trình
- Bài 2. Phương trình bậc nhất một ẩn và cách giải
- Bài 3. Phương trình đưa được về dạng ax + b = 0
- Bài 4. Phương trình tích
- Bài 5. Phương trình chứa ẩn ở mẫu
- Bài 6. Giải bài toán bằng cách lập phương trình
- Bài 7. Giải bài toán bằng cách lập phương trình (tiếp)
- Ôn tập chương III: Phương trình bậc nhất một ẩn
-
CHƯƠNG IV. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
-
PHẦN HÌNH HỌC - TOÁN 8 TẬP 2
-
CHƯƠNG III. TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta - let trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta - let
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất
- Bài 6. Trường hợp đồng dạng thứ hai
- Bài 7. Trường hợp đồng dạng thứ ba
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Bài 9. Ứng dụng thực tế của tam giác đồng dạng
- Ôn tập chương III: Tam giác đồng dạng
-
CHƯƠNG IV. HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương IV: Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM - TOÁN 8
-
-
Đề thi học kì 2 mới nhất có lời giải
-
Đề cương ôn tập học kì 2
-
Câu hỏi tự luyện Toán 8
-
Tải 30 đề kiểm tra giữa kì 1 Toán 8
-
Tải 30 đề ôn tập kiểm tra học kì 1 Toán 8
-
Tải 30 đề thi học kì 1 của các trường Toán 8
-
Tải 30 đề kiểm tra giữa kì 2 Toán 8
-
Tải 30 đề ôn tập học kì 2 Toán 8
-
Tải 30 đề thi học kì 2 của các trường Toán 8
Lý thuyết Hình bình hành
Hình bình hành là tứ giác có các cạnh đối song song
I. Các kiến thức cần nhớ
Định nghĩa: Hình bình hành là tứ giác có các cạnh đối song song.
Ví dụ: Tứ giác \(ABCD\) là hình bình hành \( \Leftrightarrow \left\{ \begin{array}{l}AB{\rm{//}}CD\\AD{\rm{//}}BC\end{array} \right.\)
Tính chất:
Trong hình bình hành:
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Chú ý: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song)
Ví dụ:
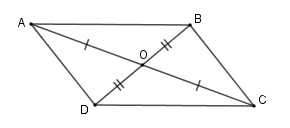
+Tứ giác \(ABCD\) là hình bình hành nên \(\left\{ \begin{array}{l}AB = DC;\,AD = BC\\AB{\rm{//}}DC{\rm{;}}\,AD{\rm{//}}BC\\\widehat A = \widehat C;\,\widehat B = \widehat D\\OA = OC;\,OB = OD\end{array} \right.\)
II. Các dạng toán thường gặp
Dạng 1: Vận dụng tính chất hình bình hành để chứng minh tính chất hình học và tính toán.
Phương pháp:
Sử dụng tính chất hình bình hành:
Trong hình bình hành:
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Dạng 2: Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình bình hành.
Phương pháp:
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Bình luận
Chia sẻ
- Trả lời câu hỏi 1 Bài 7 trang 90 SGK Toán 8 Tập 1
- Trả lời câu hỏi 2 Bài 7 trang 90 SGK Toán 8 Tập 1
- Trả lời câu hỏi 3 Bài 7 trang 92 SGK Toán 8 Tập 1
- Bài 43 trang 92 SGK Toán 8 tập 1
- Bài 44 trang 92 SGK Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
