Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 1 - Hình học 8
Giải Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 1 - Hình học 8
Đề bài
Gọi E, F lần lượt là trung điểm của AB và CD của hình bình hành ABCD.
a) Chứng minh \(AF//CE.\)
b) Chứng minh rằng AF và CE chia đường chéo BD thành ba phần bằng nhau.
Phương pháp giải - Xem chi tiết
Sử dụng:
Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành
Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó
Lời giải chi tiết
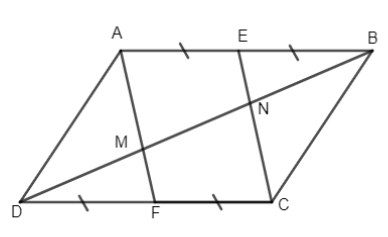
a) Ta có E, F lần lượt là trung điểm của AB và CD mà AB = CD và \(AB// CD(gt)\)
\( \Rightarrow AE = CF\) và \(AE//CF\) . Do đó AECF là hình bình hành \( \Rightarrow AF//CE.\)
b) Gọi M, N theo thứ tự là giao điểm của AF, CE với BD.
Ta có E là trung điểm của AB, \(EN// AM\left( {AF//CE} \right) \Rightarrow EN\) là đường trung bình của \(\Delta ABM \Rightarrow N\) là trung điểm của BM hay BN = NM.
Chứng minh tương tự, xét tam giác DNC, ta có F là trung điểm của DC, \(NC// MF\left( {AF//CE} \right)\)
Do đó, MF là đường trung bình của \(\Delta DNC \Rightarrow MN = MD.\)
Vậy BN = NM = MD.
(Bạn có thể giải cách khác bằng cách nối A với C. Khi đó M, N lần lượt là trọng tâm của các tam giác ADC và BAC. Gọi I là giao điểm của hai đường chéo AC và BD ta có \(BN = 2NI=\frac{2}{3}. BI\); \(DM=2MI =\frac{2}{3}. DI\), BI=DI).
Loigiaihay.com
- Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 8 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 9 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 1 - Hình học 8
>> Xem thêm













Danh sách bình luận