Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 8
Giải Đề kiểm tra 15 phút - Đề số 6 - Bài 6 - Chương 2 - Hình học 8
Đề bài
Cho hình thang ABCD \(\left( {AB//CD} \right)\). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng: \({S_{AOD}} = {S_{BOC}}.\)
b) Gọi M là trung điểm của BC. Từ M kẻ đường thẳng song song với AD cắt AB tại E và DC tại F.
Chứng minh rằng: \({S_{ABCD}} = {S_{AEFD}}.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
Diện tích tam giác bằng nửa tích đường cao với cạnh đáy tương ứng
Các tam giác bằng nhau có diện tích bằng nhau
Lời giải chi tiết
a)
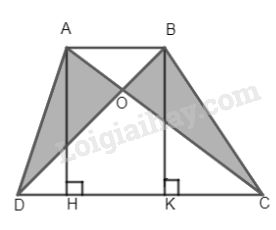
Ta có \({S_{ADC}} = {S_{DBC}}\) (chung đáy DC và đường cao AH = BK)
\( \Rightarrow {S_{ADC}} - {S_{DOC}} = {S_{DBC}} - {S_{DOC}}\)
Hay \({S_{AOD}} = {S_{BOC}}.\)
b)
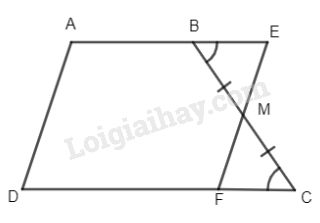
Ta có: \(\Delta BME = \Delta CMF(g.c.g)\)
\( \Rightarrow {S_{BME}} = {S_{CMF}}\)
\( \Rightarrow {S_{BME}} + {S_{ABMFD}} = {S_{CMF}} + {S_{ABMFD}}\)
Hay \({S_{AEFD}} = {S_{ABCD}}.\)
Loigiaihay.com
- Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 8 - Bài 6 - Chương 2 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 9 - Bài 6 - Chương 2 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 10 - Bài 6 - Chương 2 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 11 - Bài 6 - Chương 2 - Hình học 8
>> Xem thêm













Danh sách bình luận