Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 7. Hình bình hành

Bài 45 trang 92 SGK Toán 8 tập 1


Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B

Đề bài

Cho hình bình hành \(ABCD\) (\(AB > BC\)). Tia phân giác của góc \(D\) cắt \(AB\) ở \(E\), tia phân giác của góc \(B\) cắt \(CD\) ở \(F\).

a) Chứng minh rằng \(DE // BF\).

b) Tứ giác \(DEBF\) là hình gì ? Vì sao ?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Áp dụng:

+) Hình bình hành có các góc đối bằng nhau. 

+) Dấu hiệu nhận biết hình bình hành: Tứ giác có các cạnh đối song song là hình bình hành.

Lời giải chi tiết

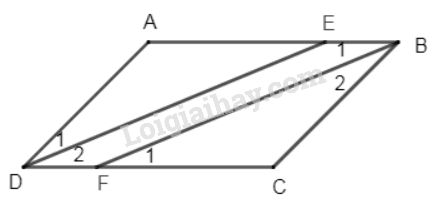
a) Vì \(ABCD\) là hình bình hành (giả thiết)

\( \Rightarrow \widehat {ABC} = \widehat {ADC}\) (tính chất hình bình hành )                       (1)

Vì \(BF\) là tia phân giác \(\widehat {ABC}\) (giả thiết)

\( \Rightarrow \)\(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\) (tính chất tia phân giác)    (2)

Vì \(DE\) là tia phân giác \(\widehat {ADC}\) (giả thiết)

\( \Rightarrow \) \(\widehat {{D_1}} = \widehat {{D_2}} = \dfrac{{\widehat {ADC}}}{2}\) (tính chất tia phân giác)   (3)

Từ (1), (2), (3) \(\Rightarrow \widehat {{D_2}} = \widehat {{B_1}}\)  (4)

Có \(AB//DC\) (vì \(ABCD\) là hình bình hành)

Suy ra: \(\widehat {{B_1}} = \widehat {{F_1}}\) (so le trong)   (5)

Từ (4) và (5) suy ra \(\widehat {{F_1}} = \widehat {{D_2}}\) mà hai góc này ở vị trí đồng vị nên \(DE//BF\) (dấu hiệu nhận biết hai đường thẳng song song)

b) \(ABCD\) là hình bình hành (giả thiết)

\( \Rightarrow \)\(AB // CD\) (tính chất hình bình hành) hay \(BE // DF\)

Xét tứ giác \(DEBF\) có \(BE // DF\) (chứng minh trên) và \(DE//BF\) (theo câu a)

Suy ra tứ giác \(DEBF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

Loigiaihay.com


Bình chọn:
4.5 trên 426 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store