Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 5. Dựng hình bằng thước và compa. Dựng hình thang

Bài 29 trang 83 SGK Toán 8 tập 1


Đề bài

Dựng \(∆ABC\) vuông tại \(A\), biết cạnh huyền \(BC = 4\,cm\), góc nhọn \(\widehat{B}={65^0}\) 

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựng \(∆ABC\) vuông tại \(A\), biết cạnh huyền \(BC = a\,cm\), góc nhọn \(\widehat{B}={x^0}\) 

Cách dựng:

- Dựng đoạn thẳng \(BC=a\,cm\)

- Dựng \(\widehat {CBx} = {x^o}\)

- Dựng \(CA\bot Bx\)

Lời giải chi tiết

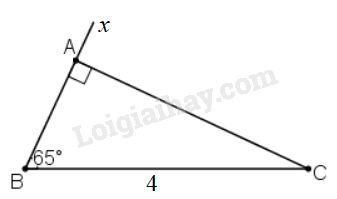
a) Phân tích

Giả sử dựng được \(ΔABC\) thỏa mãn yêu cầu đề bài.

Đoạn thẳng \(BC\) dựng được vì đã biết độ dài.

Khi đó điểm \(A\) là giao điểm của:

+ Tia \(Bx\) tạo với đoạn thẳng \(BC\) góc \({65^0}\)

+ Đường thẳng qua \(C\) và vuông góc với tia \(Bx\) vừa dựng.

b) Cách dựng

- Vẽ đoạn \(BC = 4cm.\)

- Vẽ tia \(Bx\) tạo với \(BC\) một góc \({65^0}\) 

- Vẽ đường thẳng \(a\) qua \(C\) và vuông góc với \(Bx\) và cắt \(Bx\) tại \(A.\)

Khi đó \(∆ABC\) là tam giác cần dựng.

c) Chứng minh

\(ΔABC\) vừa dựng vuông tại \(A\), \(\widehat B = {65^0}\) và \(BC = 4cm.\)

d) Biện luận

Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.

Loigiaihay.com


Bình chọn:
4.5 trên 59 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 trên Tuyensinh247.com cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua