 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Ôn tập cuối năm - Đại số - Toán 8
Ôn tập cuối năm - Đại số - Toán 8
Bài 4 trang 130 SGK Toán 8 tập 2
Rút gọn rồi tính giá trị của biểu thức sau tại
Đề bài
Rút gọn rồi tính giá trị của biểu thức sau tại \(x = - \dfrac{1}{3}\):
\(\left[ {\dfrac{{x + 3}}{{{{\left( {x - 3} \right)}^2}}} + \dfrac{6}{{{x^2} - 9}} - \dfrac{{x - 3}}{{{{\left( {x + 3} \right)}^2}}}} \right]\)\(\,.\left[ {1:\left( {\dfrac{{24{x^2}}}{{{x^4} - 81}} - \dfrac{{12}}{{{x^2} + 9}}} \right)} \right]\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Qui đồng cùng mẫu thức rồi rút gọn biểu thức.
- Thay giá trị tương ứng của \(x\) vào biểu thức sau khi đã rút gọn để tính giá trị của biểu thức đó.
Lời giải chi tiết
Điều kiện: \(x\ne \pm 3\)
+ Ngoặc vuông thứ nhất:
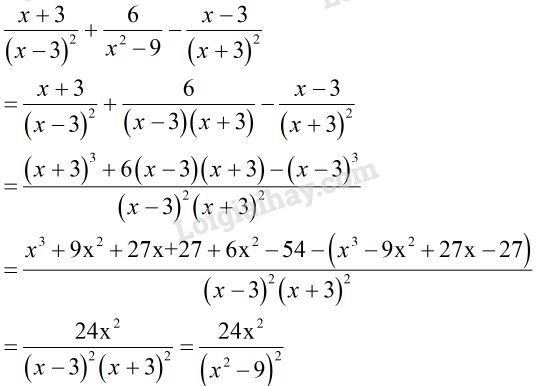
+ Ngoặc vuông thứ hai:
\(\eqalign{
& 1:\left( {{{24{x^2}} \over {{x^4} - 81}} - {{12} \over {{x^2} + 9}}} \right) \cr
& = 1:\left[ {{{24{x^2}} \over {\left( {{x^2} - 9} \right)\left( {{x^2} + 9} \right)}} - {{12} \over {{x^2} + 9}}} \right] \cr
& = 1:\left( {{{24{x^2} - 12\left( {{x^2} - 9} \right)} \over {\left( {{x^2} - 9} \right)\left( {{x^2} + 9} \right)}}} \right) \cr
& = 1:{{12{x^2} + 108} \over {\left( {{x^2} - 9} \right)\left( {{x^2} + 9} \right)}} \cr
& = 1.{{\left( {{x^2} - 9} \right)\left( {{x^2} + 9} \right)} \over {12{x^2} + 108}} \cr
& = {{\left( {{x^2} - 9} \right)\left( {{x^2} + 9} \right)} \over {12{x^2} + 108}} \cr
& = {{\left( {{x^2} - 9} \right)\left( {{x^2} + 9} \right)} \over {12\left( {{x^2} + 9} \right)}} \cr
& = {{{x^2} - 9} \over {12}} \cr} \)
Nên
\(\left[ {\dfrac{{x + 3}}{{{{\left( {x - 3} \right)}^2}}} + \dfrac{6}{{{x^2} - 9}} - \dfrac{{x - 3}}{{{{\left( {x + 3} \right)}^2}}}} \right]\)\(.\left[ {1:\left( {\dfrac{{24{{\rm{x}}^2}}}{{{x^4} - 81}} - \dfrac{{12}}{{{x^2} + 9}}} \right)} \right]\)
\(= \dfrac{{24{{\rm{x}}^2}}}{{{{\left( {{x^2} - 9} \right)}^2}}}.\dfrac{{{x^2} - 9}}{{12}} = \dfrac{{2{{\rm{x}}^2}}}{{{x^2} - 9}}\)
Tại \(x = - \dfrac{1}{3}\) giá trị của biểu thức là:
\(\dfrac{{2{{\left( { - \dfrac{1}{3}} \right)}^2}}}{{{{\left( { - \dfrac{1}{3}} \right)}^2} - 9}} = \dfrac{{2.\dfrac{1}{9}}}{{\dfrac{1}{9} - 9}} = \dfrac{{\dfrac{2}{9}}}{{ - \dfrac{{80}}{9}}} \)\(\,= - \dfrac{1}{{40}}\)
Loigiaihay.com












Danh sách bình luận