-
PHẦN ĐẠI SỐ - TOÁN 8 TẬP 1
-
CHƯƠNG I. PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3. Những hằng đẳng thức đáng nhớ
- Bài 4. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 5. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Ôn tập chương I: Phép nhân và phép chia các đa thức
- Đề kiểm tra 15 phút - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Đại số 8
-
CHƯƠNG II. PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Ôn tập chương II: Phân thức đại số
- Đề kiểm tra 15 phút – Chương 2 – Đại số 8
- Đề kiểm tra 45 phút (1 tiết ) – Chương 2 – Đại số 8
-
-
PHẦN HÌNH HỌC - TOÁN 8 TẬP 1
-
CHƯƠNG I. TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương I: Tứ giác
- Đề kiểm tra 15 phút - Chương 1 - Hình học 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 8
-
CHƯƠNG II. ĐA GIÁC, DIỆN TÍCH ĐA GIÁC
- Bài 1. Đa giác. Đa giác đều
- Bài 2. Diện tích hình chữ nhật
- Bài 3. Diện tích tam giác
- Bài 4. Diện tích hình thang
- Bài 5. Diện tích hình thoi
- Bài 6. Diện tích đa giác
- Ôn tập chương II: Đa giác. Diện tích đa giác
- Đề kiểm tra 15 phút - Chương 2 - Hình học 8
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 8
-
-
Đề cương ôn tập học kì 1 toán 8
-
Đề thi học kì 1 mới nhất có lời giải
-
PHẦN ĐẠI SỐ - TOÁN 8 TẬP 2
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
- Bài 1. Mở đầu về phương trình
- Bài 2. Phương trình bậc nhất một ẩn và cách giải
- Bài 3. Phương trình đưa được về dạng ax + b = 0
- Bài 4. Phương trình tích
- Bài 5. Phương trình chứa ẩn ở mẫu
- Bài 6. Giải bài toán bằng cách lập phương trình
- Bài 7. Giải bài toán bằng cách lập phương trình (tiếp)
- Ôn tập chương III: Phương trình bậc nhất một ẩn
-
CHƯƠNG IV. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
-
PHẦN HÌNH HỌC - TOÁN 8 TẬP 2
-
CHƯƠNG III. TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta - let trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta - let
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất
- Bài 6. Trường hợp đồng dạng thứ hai
- Bài 7. Trường hợp đồng dạng thứ ba
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Bài 9. Ứng dụng thực tế của tam giác đồng dạng
- Ôn tập chương III: Tam giác đồng dạng
-
CHƯƠNG IV. HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương IV: Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM - TOÁN 8
-
-
Đề thi học kì 2 mới nhất có lời giải
-
Đề cương ôn tập học kì 2
-
Câu hỏi tự luyện Toán 8
-
Tải 30 đề kiểm tra giữa kì 1 Toán 8
-
Tải 30 đề ôn tập kiểm tra học kì 1 Toán 8
-
Tải 30 đề thi học kì 1 của các trường Toán 8
-
Tải 30 đề kiểm tra giữa kì 2 Toán 8
-
Tải 30 đề ôn tập học kì 2 Toán 8
-
Tải 30 đề thi học kì 2 của các trường Toán 8
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Ôn tập cuối năm - Đại số - Toán 8
Bài 10 trang 131 SGK Toán 8 tập 2
Giải các phương trình:
Video hướng dẫn giải
Giải các phương trình:
LG a.
\(\dfrac{1}{{x + 1}} - \dfrac{5}{{x - 2}} = \dfrac{{15}}{{\left( {x + 1} \right)\left( {2 - x} \right)}}\)
Phương pháp giải:
- Tìm điều kiện xác định.
- Qui đồng khử mẫu.
- Rút gọn rồi tìm nghiệm \(x\).
- Đối chiếu với điều kiện xác định rồi kết luận nghiệm.
Lời giải chi tiết:
\(\dfrac{1}{{x + 1}} - \dfrac{5}{{x - 2}} = \dfrac{{15}}{{\left( {x + 1} \right)\left( {2 - x} \right)}}\)
ĐKXĐ: \(x \ne - 1;x \ne 2\)
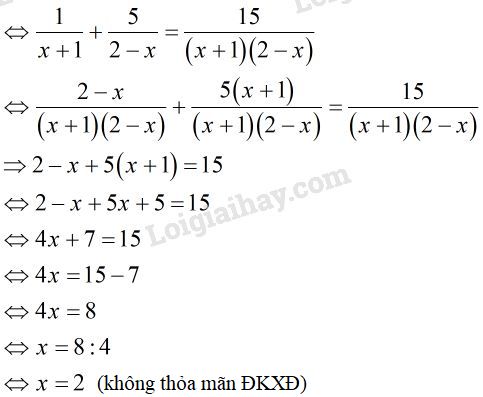
Vậy phương trình vô nghiệm.
LG b.
\(\dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} = \dfrac{{5x - 2}}{{4 - {x^2}}}\)
Phương pháp giải:
- Tìm điều kiện xác định.
- Qui đồng khử mẫu.
- Rút gọn rồi tìm nghiệm \(x\).
- Đối chiếu với điều kiện xác định rồi kết luận nghiệm.
Lời giải chi tiết:
\(\dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} = \dfrac{{5x - 2}}{{4 - {x^2}}}\)
ĐKXĐ:\(x \ne \pm 2\)
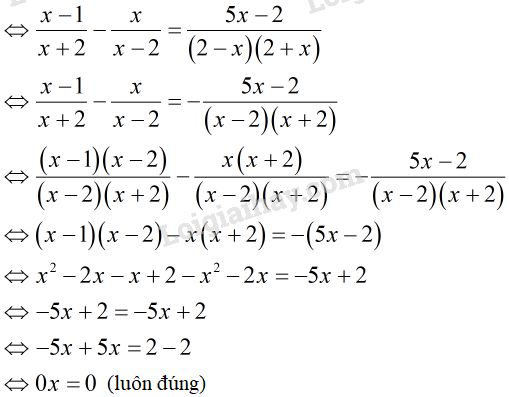
Vậy phương trình nghiệm đúng với mọi \(x \ne \pm 2\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 11 trang 131 SGK Toán 8 tập 2
- Bài 12 trang 131 SGK Toán 8 tập 2
- Bài 13 trang 131 SGK Toán 8 tập 2
- Bài 14 trang 131 SGK Toán 8 tập 2
- Bài 15 trang 131 SGK Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
