Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 1. Một số hệ thức về cạnh và đường cao trong tam gi..

Trả lời câu hỏi 1 Bài 1 trang 66 SGK Toán 9 Tập 1


Xét hình 1. Chứng minh

Đề bài

Xét hình 1. Chứng minh \(\Delta AHB \sim \Delta CHA\). Từ đó suy ra hệ thức (2) là \(h^2=b'c'.\)


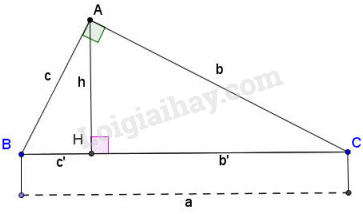
                            Hình 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng trường hợp đồng dạng góc-góc để chứng minh hai tam giác \(ABH\) và \(CAH\) đồng dạng.

Từ đó suy ra tỉ lệ cạnh và hệ thức cần tìm. 

Lời giải chi tiết

Ta có \(\widehat {BAH} + \widehat {CAH}=90^0\) và \(\widehat {CAH} + \widehat {ACH}=90^0\) (do tam giác \(AHC\) vuông tại \(H\))

Do đó \(\widehat {BAH} = \widehat {ACH}\) (cùng phụ \(\widehat {CAH}\))

Xét  \(\Delta ABH\) và  \(\Delta CAH\) có:

\(\widehat {AHB} = \widehat {AHC}( = {90^o}\))

\(\widehat {BAH} = \widehat {ACH}\) (chứng minh trên )

\( \Rightarrow \Delta ABH \sim \Delta CAH\,\,\left( {g.g} \right)\) 

\( \displaystyle \Rightarrow {{AH} \over {CH}} = {{BH} \over {AH}}\)( cặp cạnh tương ứng tỉ lệ)

\(\Rightarrow A{H^2} = BH.CH\,\,hay\,\,{h^2} = b' . c'\)


Bình chọn:
4.6 trên 66 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store