Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 1. Một số hệ thức về cạnh và đường cao trong tam gi..

Lý thuyết một số hệ thức về cạnh và đường cao trong tam giác vuông


Lý thuyết một số hệ thức về cạnh và đường cao trong tam giác vuông

1. Hệ thức về cạnh và đường cao trong tam giác vuông 

Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) (hình vẽ). Khi đó ta có các hệ thức sau:

 

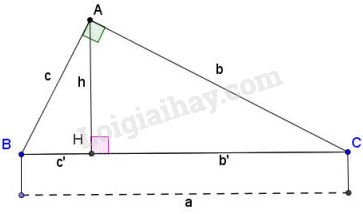
+) \(A{B^2} = BH.BC\) và \(A{C^2} = CH.BC\) hay \({c^2} = a.c'\) và \({b^2} = ab'\) (1)

+) \(H{A^2} = HB.HC\) hay \({h^2} = c'b'\) (2)

+) \(AB.AC = BC.AH\) hay \(cb = ah\) (3)

+) \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\) hay \(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}\) (4).

+) \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago). 

2. Các dạng toán cơ bản

Dạng 1: Tính độ dài các đoạn thẳng trong tam giác vuông

Phương pháp:

Sử dụng hệ thức về cạnh và đường cao trong tam giác vuông.

Dạng 2: Chứng minh các hệ thức liên quan giữa các yếu tố trong tam giác vuông

Phương pháp:

Ta thường sử dụng các kiến thức:

- Đưa về hai tam giác đồng dạng có chứa các đoạn thẳng có trong hệ thức.

- Sử dụng các hệ thức về cạnh và đường cao trong tam giác vuông để chứng minh.

Loigiaihay.com


Bình chọn:
4.7 trên 83 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store