Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 1. Một số hệ thức về cạnh và đường cao trong tam gi..

Bài 8 trang 70 SGK Toán 9 tập 1


Tìm x và y trong mỗi hình sau

Đề bài

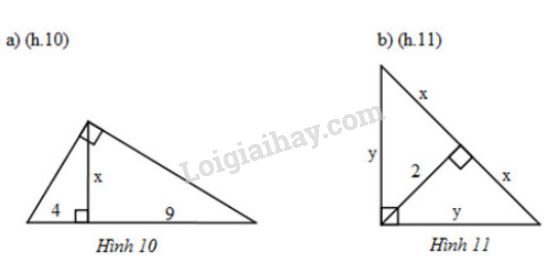
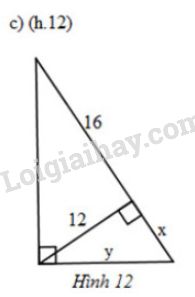
Tìm \(x\) và \(y\) trong mỗi hình sau:

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Dùng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\), biết \(b',\ c'\) tính được \(h\).

b) +) Dùng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\)

+) Dùng định lí Pytago trong tam giác vuông để tính \(y\).

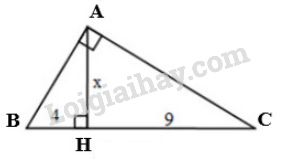
c) Dùng hệ thức liên quan đến đường cao và hình chiếu \(h^2=b'.c'\), biết \(h,\ b'\) tính được \(c'\).

+) Dùng định lí Pytago trong tam giác vuông.

Lời giải chi tiết

 Đặt tên các điểm như hình vẽ:

Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:

                           \(AH^2=BH.CH \)

                     \(\Leftrightarrow x^2=4.9=36\)

                     \(\Leftrightarrow x=\sqrt{36}=6\)

Vậy \(x=6\)

b) Đặt tên các điểm như hình vẽ

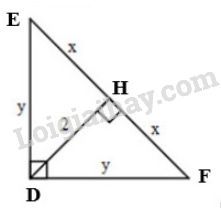
Xét \(\Delta{DEF}\) vuông tại \(D\), đường cao \(DH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:

\(D{H^2} = HE.HF \Rightarrow {2^2} = x.x \Rightarrow {x^2} = 4 \Rightarrow x = 2\)

Xét \(\Delta{DHF}\) vuông tại \(H\). Áp dụng định lí Pytago, ta có:

\(DF^2=DH^2+HF^2\)

\({y^2} = {2^2} + {x^2} = {2^2} + {2^2} = 8 \)

\(\Rightarrow y = \sqrt 8  = 2\sqrt 2 \)

Vậy \(x= 2,\ y=2\sqrt 2\).

c) Đặt tên các điểm như hình vẽ:

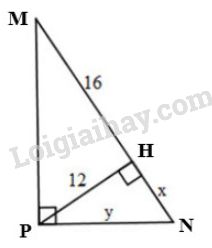
Xét \(\Delta{MNP}\) vuông tại \(P\), đường cao \(PH\). Áp dụng hệ thức \(h^2=b'.c'\), ta được:

              \(PH^2=HM.HN \Leftrightarrow 12^2=16.x\)

                                              \(\Leftrightarrow 144=16.x\)

                                              \(\Leftrightarrow x=\dfrac{144}{16}=9\)

 Xét \(\Delta{PHN}\) vuông tại \(H\). Áp dụng định lí Pytago, ta có:

\(PN^2=PH^2+HN^2 \Leftrightarrow y^2=12^2+9^2\)

\(\Leftrightarrow y^2=144+81=225\)

\(\Leftrightarrow y= \sqrt{225}=15\)

Vậy \(x=9,\ y=15\).

Loigiaihay.com


Bình chọn:
4.6 trên 199 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store