Bài 75 trang 106 SGK Toán 8 tập 1
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.
Đề bài
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng dấu hiệu nhận biết hình thoi: Tứ giác có bốn cạnh bằng nhau là hình thoi.
Lời giải chi tiết
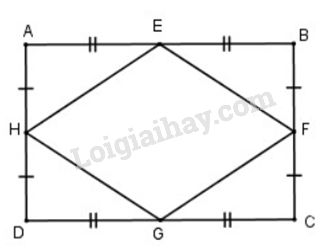
Giả sử hình chữ nhật \(ABCD\) có \(E,F,G,H\) lần lượt là trung điểm của \(AB,BC,CD,DA\)
Bốn tam giác vuông \(EAH, EBF, GDH, GCF\) có:
\(AE = BE = DG = CG\) ( = \(\dfrac{1}{2}AB\) = \(\dfrac{1}{2}CD\) )
\(HA = FB = DH = CF\) ( = \(\dfrac{1}{2}AD = \dfrac{1}{2}BC\) )
Xét \(∆EAH\) và \(∆EBF\) có:
\(\left\{ \begin{array}{l}
A{\rm{E}} = BE\left( {cmt} \right)\\
\widehat A = \widehat B = {90^0}\left( {gt} \right)\\
AH = BF\left( {cmt} \right)
\end{array} \right.\)
\( \Rightarrow \Delta AHE = \Delta BEF\left( {c - g - c} \right)\)
\( \Rightarrow \) \(EH = EF \) (2 cạnh tương ứng) (1)
Xét \(∆HDG\) và \(∆FCG\) có:
\(\left\{ \begin{array}{l}
H{\rm{D}} = FC\left( {cmt} \right)\\
\widehat D = \widehat C = {90^0}\left( {gt} \right)\\
DG = CG\left( {cmt} \right)
\end{array} \right.\)
\( \Rightarrow \Delta HDG = \Delta FCG\left( {c - g - c} \right)\)
\( \Rightarrow \) \(GH = GF \) (2 cạnh tương ứng) (2)
Xét \(∆AHE\) và \(∆DHG\) có:
\(\left\{ \begin{array}{l}
H{\rm{A}} = HD\left( {cmt} \right)\\
\widehat A = \widehat D = {90^0}\left( {gt} \right)\\
AE = DG\left( {cmt} \right)
\end{array} \right. \)
\(\Rightarrow \Delta AHE = \Delta DHG\left( {c - g - c} \right)\)
\( \Rightarrow \) \(EH = HG \) (2 cạnh tương ứng) (3)
Từ (1), (2) và (3) \( \Rightarrow HE=EF = HG = GF\)
\( \Rightarrow \) \(EFGH\) là hình thoi (dấu hiệu nhận biết hình thoi).
(Trong đó: "cmt" là chứng minh trên)
Cách khác:
* Xét tam giác \(ABD\) có \(E\) và \(H\) lần lượt là trung điểm của \(AB\) và \(AD\)
Suy ra \(EH\) là đường trung bình của tam giác
Từ đó \(EH=\dfrac{BD}2\) (*)
Chứng minh tương tự ta có: \(GF=\dfrac{BD}2\), \(EF=\dfrac{AC}2\), \(HG=\dfrac{AC}2\) (**)
Vì \(ABCD\) là hình chữ nhật nên \(AC=BD\) (***) (tính chất)
Từ (*), (**), (***) ta suy ra \(EH=EF=HG=GF\)
\( \Rightarrow \) \(EFGH\) là hình thoi (dấu hiệu nhận biết hình thoi).
Loigiaihay.com













Danh sách bình luận