Bài 30 trang 107 SBT toán 9 tập 1
Giải bài 30 trang 107 sách bài tập toán 9. Đường cao MQ của tam giác vuông MNP chia cạnh huyền NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotgN và cotgP. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
Đề bài
Đường cao \(MQ\) của tam giác vuông MNP chia cạnh huyền \(NP\) thành hai đoạn \(NQ = 3, PQ = 6\). Hãy so sánh \(cotgN\) và \(cotgP\). Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
Phương pháp giải - Xem chi tiết
Các tỉ số lượng giác của góc nhọn (hình vẽ) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết
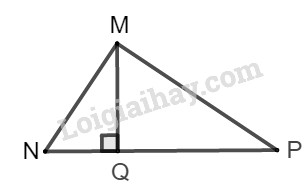
Tam giác \(MNQ\) vuông tại \(Q\) nên ta có:
\(\cot g\widehat N = \dfrac{{NQ}}{{MQ}} = \dfrac{3}{{MQ}}\)
Tam giác \(MPQ\) vuông tại \(Q\) nên ta có:
\(\cot g\widehat P = \dfrac{{PQ}}{{MQ}} = \dfrac{6}{{MQ}}\)
Ta có: \( \dfrac{6}{{MQ}} > \dfrac{3}{{MQ}}\) nên \(\cot g\widehat P > \cot g\widehat N\)
\( \dfrac{{\cot g\widehat P}}{{\cot g\widehat N}} = \dfrac{{\dfrac{6}{{MQ}}}}{{\dfrac{3}{{MQ}}}}\) = \(\dfrac{6}{ {MQ}}.\dfrac{{MQ}}{3}\) = \(\dfrac{6}{3} = 2\)
Vậy \(\cot g\widehat P = 2\cot g\widehat N.\)
Loigiaihay.com













Danh sách bình luận