Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 3 - Hình học 9
Đề bài
Cho tam giác ABC nội tiếp trong đường tròn (O). Từ một điểm bất kì trên đường tròn hạ các đường vuông góc xuống các cạnh. Chứng minh rằng chân ba đường vuông góc này thẳng hàng (đường thẳng Sim-Sơn).
Phương pháp giải - Xem chi tiết
Gọi chân các đường vuông góc hạ từ M lần lượt xuống các cạnh AB, BC, CA là H, K, I. Chứng minh \(\widehat {MIK} + \widehat {HIM} = 180^\circ \)
Lời giải chi tiết
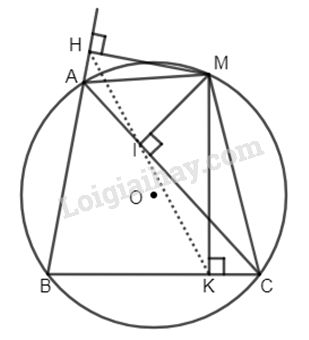
Gọi chân các đường vuông góc hạ từ M lần lượt xuống các cạnh AB, BC, CA là H, K, I.
Ta có tứ giác AHMI nội tiếp ( vì có \(\widehat {AHM} + \widehat {AIM} = 180^\circ \))
\( \Rightarrow \widehat {HAM} = \widehat {HIM}\) (1) ( góc nội tiếp cung chắn MH)
Tương tự tứ giác CKIM nội tiếp ( vì \(\widehat {CKM} + \widehat {CIM} = 90^\circ \))
\( \Rightarrow \widehat {MIK} + \widehat {MCK} = 180^\circ \) (2)
Mặt khác ABCM nội tiếp (O) nên \(\widehat {HAM} = \widehat {MCK}\)
Suy ra \(\widehat {HIM} = \widehat {MCK}\)
Do đó \(\widehat {MIK} + \widehat {HIM} = 180^\circ \)
\(\Rightarrow H, I, K\) thẳng hàng.
Trường hợp M thuộc các cung còn lại chứng minh tương tự.
Loigiaihay.com
- Đề kiểm tra 15 phút - Đề số 9 - Bài 7 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 8 - Bài 7 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 3 - Hình học 9
- Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 3 - Hình học 9
>> Xem thêm
Các bài khác cùng chuyên mục













Danh sách bình luận