Bài 53 trang 89 SGK Toán 9 tập 2
Biết ABCD là tứ giác nội tiếp
Đề bài
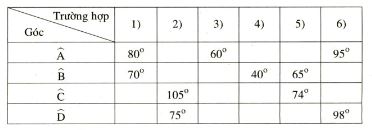
Biết \(ABCD\) là tứ giác nội tiếp. Hãy điền vào ô trống trong bẳng sau (nếu có thể).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Trong tứ giác nội tiếp, tổng số đo hai góc đối diện bằng \(180^0.\)
Lời giải chi tiết
Theo đề bài ta có \(ABCD\) là tứ giác nội tiếp \( \Rightarrow \left\{ \begin{array}{l}\widehat A + \widehat C = {180^0}\\\widehat B + \widehat D = {180^0}\end{array} \right..\)
- Trường hợp 1:
Ta có: \(\widehat A + \widehat C = {180^0}\)
\(\Rightarrow \widehat C = {180^0}-\widehat A= {180^0} - {80^0} = {100^0}.\)
\(\widehat B + \widehat D = {180^0} \)
\(\Rightarrow \widehat D = {180^0} - \widehat B = {180^0} - {70^0} = {110^0}.\)
Vậy các góc còn lại là: \(\widehat{C}= 100^0,\) \(\widehat{D} = 110^0.\)
- Trường hợp 2:
\(\begin{array}{l} Ta \, \, có: \, \,
\widehat A + \widehat C = {180^0} \\\Rightarrow \widehat A = {180^0} - \widehat C = {180^0} - {105^0} = {75^0}.\\
\widehat B + \widehat D = {180^0}\\ \Rightarrow \widehat B = {180^0} - \widehat D = {180^0} - {75^0} = {105^0}.
\end{array}\)
- Trường hợp 3:
Ta có: \(\widehat A + \widehat C = {180^0} \)
\(\Rightarrow \widehat C = {180^0}-\widehat A= {180^0} - {60^0} = {120^0}.\)
Có \( \widehat B + \widehat D = {180^0}.\)
Gọi \(\widehat{B} = x^0\) thì \(\widehat{D}=180^0-x^0\)
- Trường hợp 4: \(\widehat{D}=180^0-\widehat{B}=180^0 – 40^0= 140^0.\)
Còn lại \(\widehat{A}+ \widehat{C}= 180^0.\)
Gọi \(\widehat{A} = y^0\) thì \(\widehat{C}=180^0-y^0\)
- Trường hợp 5: \(\widehat{A}=180^0-\widehat{C}=180^0–74^0=106^0.\)
\(\widehat{B}= 180^0-\widehat{D}=180^0–65^0=115^0.\)
- Trường hợp 6: \(\widehat{C}=180^0-\widehat{A}=180^0–95^0=85^0.\)
\(\widehat{B}=180^0-\widehat{D}=180^0– 98^0=82^0.\)
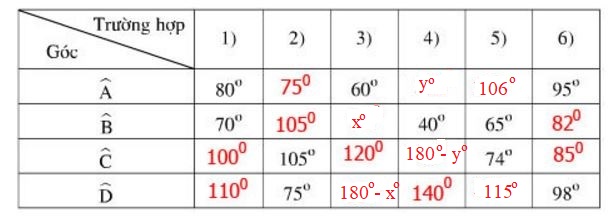
Vậy điền vào ô trống ta được bảng sau:
Các bài khác cùng chuyên mục













Danh sách bình luận