Bài 54 trang 89 SGK Toán 9 tập 2
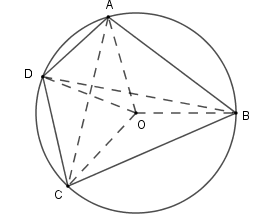
Tứ giác ABCD
Đề bài
Tứ giác \(ABCD\) có \(\widehat{ABC}+ \widehat{ADC}= 180^0\). Chứng minh rằng các đường trung trực của \(AC,\, BD, \,AB\) cùng đi qua một điểm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Nếu một tứ giác có tổng số đo hai góc đối diện bằng \(180^0\) thì tứ giác đó là tứ giác nội tiếp.
+) Các điểm thuộc đường trung trực của một đoạn thẳng đều cách đều hai đầu mút của đoạn thẳng đó.
Lời giải chi tiết
Tứ giác \(ABCD\) có \(\widehat{ABC}+ \widehat{ADC}= 180^0\) mà hai góc \(\widehat{ABC}\) và \( \widehat{ADC}\) là hai góc ở vị trí đối nhau nên tứ giác \(ABCD\) là tứ giác nội tiếp.
Gọi \(O\) là tâm đường tròn ngoại tiếp tứ giác \(ABCD\), khi đó \(OA=OB=OC=OD\) (cùng bằng bán kính của đường tròn \( (O) \) )
+ Vì \(OA = OB\) nên \(O\) thuộc đường trung trực của đoạn \(AB\) (định lí)
+ Vì \(OA = OC\) nên \(O\) thuộc đường trung trực của đoạn \(AC\) (định lí)
+ Vì \(OD = OB\) nên \(O\) thuộc đường trung trực của đoạn \(BD\) (định lí)
Do đó các đường trung trực của \(AB, \, BD, \, AC\) cùng đi qua tâm \(O\) của đường tròn ngoại tiếp tứ giác \(ABCD\).
Các bài khác cùng chuyên mục













Danh sách bình luận