Bài 58 trang 90 SGK Toán 9 tập 2

Cho tam giác đều ABC.

Đề bài

Cho tam giác đều $ABC.$ Trên nửa mặt phẳng bờ $BC$ không chứa đỉnh $A,$ lấy điểm $D$ sao cho $DB = DC$ và $\widehat{DCB}=\dfrac{1}{2}\widehat{ACB}.$

a) Chứng minh $ABDC$ là tứ giác nội tiếp.

b) Xác định tâm của đường tròn đi qua bốn điểm $A,\, B,\, D, \,C$ .

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a ) +) Tứ giác có tổng hai góc đối diện bằng $180^0$ thì tứ giác đó là tứ giác nội tiếp.

+) Sử dụng tính chất tam giác đều, tính chất tam giác cân

b) Trong tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm cạnh huyền

Lời giải chi tiết

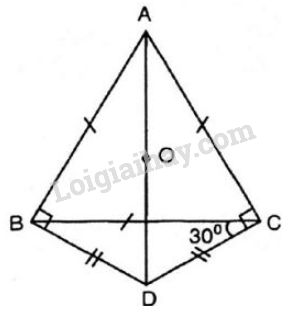
a) Vì tam giác ABC đều (gt) nên $\widehat{ACB}=60^0$

$\Rightarrow$ $\widehat{DCB}=\dfrac{1}{2}\widehat{ACB} = \dfrac{1}{2} .60^0= 30^0.$

$\widehat{ACD}=\widehat{ACB} +\widehat{BCD}$ (tia $CB$ nằm giữa hai tia $CA,\, CD$ )

$\Rightarrow$ $\widehat{ACD}=60^0+ 30^0=90^0$ (1)

Do $DB = CD$ nên $∆BDC$ cân tại $D$ $\Rightarrow \widehat{DBC} = \widehat{DCB} = 30^0$

Từ đó $\widehat{ABD}= 30^0+60^0=90^0$ (2)

Từ (1) và (2) có $\widehat{ACD}+ \widehat{ABD}=180^0$ nên tứ giác $ABDC$ là tứ giác nội tiếp.

b) Vì $\widehat{ABD} = 90^0$ nên $AD$ là đường kính của đường tròn ngoại tiếp tam giác ABD. Mà ABDC là tứ giác nội tiếp nên $AD$ cũng là đường kính của đường tròn ngoại tiếp tứ giác ABDC. Vậy tâm đường tròn ngoại tiếp tứ giác $ABDC$ là trung điểm $AD.$

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 135 phiếu

Bài tiếp theo

Bài 59 trang 90 SGK Toán 9 tập 2
Cho hình bình hành ABCD
Bài 60 trang 90 SGK Toán 9 tập 2
Xem hình 48. Chứng minh QR // ST.
Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 3 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 4 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 7 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 8 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 8 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 9 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 9 - Bài 7 - Chương 3 - Hình học 9
Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 3 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 10 - Bài 7 - Chương 3 - Hình học 9
Bài 57 trang 89 SGK Toán 9 tập 2
Trong các hình sau
Bài 56 trang 89 SGK Toán 9 tập 2
Giải bài 56 trang 89 SGK Toán 9 tập 2. Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD
Bài 55 trang 89 SGK Toán 9 tập 2
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M
Bài 54 trang 89 SGK Toán 9 tập 2
Tứ giác ABCD
Bài 53 trang 89 SGK Toán 9 tập 2
Biết ABCD là tứ giác nội tiếp
Trả lời câu hỏi Bài 7 trang 88 Toán 9 Tập 2
Trả lời câu hỏi Bài 7 trang 88 Toán 9 Tập 2. Xem hình 45. Hãy chứng minh định lý trên.
Trả lời câu hỏi Bài 7 trang 87 Toán 9 Tập 2
Trả lời câu hỏi Bài 7 trang 87 Toán 9 Tập 2. a) Vẽ một đường tròn tâm O rồi vẽ một tứ giác có tất cả các đỉnh nằm trên đường tròn đó.
Lý thuyết tứ giác nội tiếp
Định nghĩa tứ giác nội tiếp

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com

>> Chi tiết khoá học xem: TẠI ĐÂY

Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.