 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Ôn tập cuối năm - Hình học - Toán 8
Ôn tập cuối năm - Hình học - Toán 8
Bài 11 trang 132 SGK Toán 8 tập 2
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 20 cm, cạnh bên SA = 24cm.
Đề bài
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy \(AB = 20\, cm\), cạnh bên \(SA = 24\,cm.\)
a) Tính chiều cao \(SO\) rồi tính thể tích của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính thể tích và diện tích toàn phần của hình chóp tứ giác đều.
Lời giải chi tiết
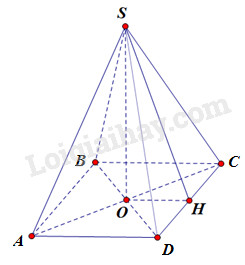
a) Vì \(S.ABCD\) là hình chóp tứ giác đều nên \(ABCD\) là hình vuông.
Do đó, \(B{\rm{D}} = \sqrt{AB^2+AD^2}\)\(=\sqrt{20^2+20^2} = 20\sqrt 2 \,cm\)
Vì \(SO\) là đường cao nên \(SO \bot \left( {ABC{\rm{D}}} \right)\) hay \(\Delta {\rm{OSD}}\) vuông tại \(O.\)
Áp dụng định lí Pitago ta có:
\(S{O^2} = S{D^2} - O{D^2} \)\(\,= {24^2} - {\left( {\dfrac{{20\sqrt 2 }}{2}} \right)^2}\) \( = 376\)
\( \Rightarrow SO=\sqrt{376} \approx 19,4\left( {cm} \right)\)
\(V =\dfrac{1}{3}{.20^2}.\sqrt{376}\approx 2585,43\) (cm3)
b) Gọi \(H\) là trung điểm của \(CD\). Suy ra SH vuông góc với CD (do tam giác SCD cân tại S)
Xét tam giác SHD vuông tại H, theo định lý Pytago ta có:
\(S{H^2} = S{D^2} - D{H^2} = {24^2} - {\left( {\dfrac{{20}}{2}} \right)^2} \) \(= 476\)
\( \Rightarrow SH=\sqrt {476} ≈ 21,8 (cm)\)
\({S_{xq}} = p.d = \dfrac{1}{2}.4.20.\sqrt {476} \approx 872,7\) (cm2)
\({S_đ} = A{B^2} = {20^2} = 400\left( {c{m^2}} \right)\)
\({S_{tp}} = {S_{xq}} + {S_đ} = 872,7 + 400 = 1272,7\) \({\left( {cm} \right)^2}\)
Loigiaihay.com











Danh sách bình luận