Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Đề ôn tập học kì 1 – Có đáp án và lời giải

Đề số 7 - Đề kiểm tra học kì 1 - Toán 8

Tải về

Đáp án và lời giải chi tiết Đề số 7 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 8

Lựa chọn câu để xem lời giải nhanh hơn

Đề bài

Bài 1 (2 điểm)Phân tích các đa thức sau thành nhân tử:

a)\(2{x^3}y - 50xy\)

b)\({x^2} - 6x - 4{y^2} + 9\)

Bài 2 (1 điểm)Thực hiện phép tính:

a)\(\left( {x - 3} \right)\left( {{x^2} + 4x + 5} \right)\)

b)\(\left( {2{x^3} - 4{x^2} - 5x + 7} \right):\left( {x - 1} \right)\)

Bài 3 (2,5 điểm)Tìm số thực\(x\), biết:

a)\(2{x^3} - 2{x^2} + 2017x - 2017 = 0\)

b)\(2{x^2} + 4x = 0\)

Bài 4 (2,5 điểm)Cho biểu thức \(A = \dfrac{{{x^2}}}{{{x^2} - 4}} - \dfrac{x}{{x - 2}} + \dfrac{2}{{x + 2}}\)

a)Tìm điều kiện của \(x\) để biểu thức xác định.

b)Rút gọn biểu thức A.

c)Tính giá trị của biểu thức A khi \(\left| {2x - 1} \right| = 1\).

Bài 5 (4 điểm)Cho \(\Delta MNP\) vuông tại \(M\), đường cao \(MH\). Biết \(MN = 3cm,\,NP = 5cm\). Gọi \(D,\,\,E\) lần lượt là chân các đường vuông góc hạ từ\(H\) xuống \(MN\)  và \(MP\).

a)Tính diện tích \(\Delta MNP\).

b)Chứng minh tứ giác \(M{\rm{D}}HE\) là hình chữ nhật.

c)Tính độ dài đoạn \(DE\).

d)Gọi \(A\) là trung điển của \(HP\). Tính \(\angle DE{\rm{A}}\).

Bài 6 (0,5 điểm)Cho \(a + b = 1\). Tính giá trị của biểu thức:

\(S = {a^3} + {b^3} + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}\left( {a + b} \right)\)

LG bài 1

Lời giải chi tiết:

Bài 1.

\(\begin{array}{l}a)\,\,2{x^3}y - 50xy = 2xy\left( {{x^2} - 25} \right) \\= 2xy\left( {x - 5} \right)\left( {x + 5} \right)\\b)\,\,{x^2} - 6x - 4{y^2} + 9 = \left( {{x^2} - 6x + 9} \right) - 4{y^2}\\ = {\left( {x - 3} \right)^2} - {\left( {2y} \right)^2}\\ = \left( {x - 3 - 2y} \right)\left( {x - 3 + 2y} \right)\end{array}\)

LG bài 2

Lời giải chi tiết:

Bài 2:

\(\begin{array}{l}a)\,\,\left( {x - 3} \right)\left( {{x^2} + 4x + 5} \right) \\= {x^3} + 4{x^2} + 5x - 3{x^2} - 12x - 15 \\= {x^3} + {x^2} - 7x - 15\\b)\;\left( {2{x^3} - 4{x^2} - 5x + 7} \right):\left( {x - 1} \right)\\ = \left( {2{x^3} - 2{x^2} - 2{x^2} + 2x - 7x + 7} \right):\left( {x - 1} \right)\\ = \left[ {2{x^2}\left( {x - 1} \right) - 2x\left( {x - 1} \right) - 7\left( {x - 1} \right)} \right]:\left( {x - 1} \right)\\ = \left( {x - 1} \right)\left( {2{x^2} - 2x - 7} \right):\left( {x - 1} \right)\\ = 2{x^2} - 2x - 7.\end{array}\)

LG bài 3

Lời giải chi tiết:

Bài 3

\(\begin{array}{l}a)\,\,2{x^3} - 2{x^2} + 2017x - 2017 = 0\\ \Leftrightarrow 2{x^2}\left( {x - 1} \right) + 2017\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {2{x^2} + 2017} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\2{x^2} + 2017 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\2{x^2} =  - 2017\left( {vn} \right)\end{array} \right.\end{array}\)

Vậy phương trình có 1 nghiệm duy nhất \(x = 1\)

\(\begin{array}{l}b)\,\,2{x^2} + 4x = 0\\ \Leftrightarrow 2x\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.\end{array}\)

Vậy phương trình có 2 nghiệm \(x = 0\)và \(x =  - 2\)

LG bài 4

Lời giải chi tiết:

Bài 4:

\(a)\;\;A = \dfrac{{{x^2}}}{{{x^2} - 4}} - \dfrac{x}{{x - 2}} + \dfrac{2}{{x + 2}}\)

Điều kiện xác định: \(\left\{ \begin{array}{l}{x^2} - 4 \ne 0\\x - 2 \ne 0\\x + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right)\left( {x + 2} \right) \ne 0\\x \ne 2\\x \ne  - 2\end{array} \right. \Leftrightarrow x \ne  \pm 2\)

\(\begin{array}{l}b)\;\;A = \dfrac{{{x^2}}}{{{x^2} - 4}} - \dfrac{x}{{x - 2}} + \dfrac{2}{{x + 2}}\\\;\;\;\;\;\;\; = \dfrac{{{x^2} - x\left( {x + 2} \right) + 2\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\\\;\;\;\;\;\;\;\; = \dfrac{{{x^2} - {x^2} - 2x + 2x - 4}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \dfrac{{ - 4}}{{{x^2} - 4}}.\end{array}\)

c) Ta có: \(\left| {2x - 1} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}2x - 1 = 1\\2x - 1 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 0\end{array} \right.\)

Thay \(x = 1\) vào \(A\) ta có: \(\dfrac{{ - 4}}{{{x^2} - 4}} = \dfrac{{ - 4}}{{1 - 4}} = \dfrac{{ - 4}}{{ - 3}} = \dfrac{4}{3}.\)

Thay \(x = 0\) vào \(A\) ta có: \(\dfrac{{ - 4}}{{{x^2} - 4}} = \dfrac{{ - 4}}{{0 - 4}} = \dfrac{{ - 4}}{{ - 4}} = 1.\)

LG bài 5

Lời giải chi tiết:

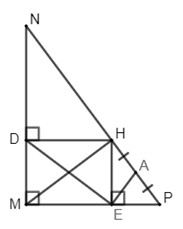
a) Xét \({\Delta }MNP\), áp dụng định lý Py-ta-go ta có:

\(M{P^2} + N{M^2} = N{P^2}\)

\(\Rightarrow M{P^2} = N{P^2} - N{M^2} = {5^2} - {3^2} = 16\)

\(\Rightarrow MP = 4\,cm.\)

Diện tích \(\Delta MNP\) có: \(\dfrac{{MP.MN}}{2} = \dfrac{{3.4}}{2} = 6\,c{m^2}\)

b) Ta có: \(\left\{ \begin{array}{l}HE \bot MP\\H{\rm{D}} \bot MN\end{array} \right.\left( {gt} \right) \Rightarrow \angle HEM = \angle H{\rm{D}}M = {90^0}\)

Xét tứ giác \(M{\rm{D}}HE\) có: \(\angle DME = \angle M{\rm{D}}H = \angle HEM = {90^0} \Rightarrow M{\rm{D}}HE\) là hình chữ nhật (dhnb)

c) Ta có: \({S_{MNP}} = \dfrac{1}{2}MN.MP = \dfrac{1}{2}MH.NP\)

\(\begin{array}{l} \Leftrightarrow MH.NP = MN.MP\\ \Leftrightarrow MH.5 = 3.4\\ \Leftrightarrow MH = \dfrac{{12}}{5} = 2,4\;cm.\end{array}\)

Lại có \(MDHE\) là hình chữ nhật (cmt) \( \Rightarrow MH = DE = 2,4\;cm\)(hai đường chéo hình chữ nhật).

d)Vì \(M{\rm{D}}HE\) là hình chữ nhật (cmt)

\( \Rightarrow \angle DEH = \angle MHE\) (tính chất hình chữ nhật)

Xét \({\Delta _v}HEP\) có \(A\) là trung điểm của \(HP\left( {gt} \right) \Rightarrow E{\rm{A}}\) là đường trung tuyến của tam giác \(HEP.\)

\( \Rightarrow E{\rm{A}} = \dfrac{{HP}}{2} = HA\) (tính chất trong tam giác vuông có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)

\( \Rightarrow \Delta HA{\rm{E}}\) là tam giác cân tại A (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow \angle AHE = \angle A{\rm{E}}H\) (tính chất tam giác cân)

Mà \(\angle MHE + \angle EHA = {90^0}\left( {gt} \right) \)

\(\Rightarrow \angle DEH + \angle A{\rm{E}}H = {90^0} \)

\(\Rightarrow \angle DE{\rm{A}} = {90^{^0}}\)

LG bài 6

Lời giải chi tiết:

Vì \(a + b = 1\) nên ta có:

\(\begin{array}{l}S = {a^3} + {b^3} + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}\left( {a + b} \right)\\\;\;\;= \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right) + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}.1\\\;\;\; = 1.\left( {{a^2} - ab + {b^2}} \right) + 3ab\left( {{a^2} + {b^2} + 2ab} \right) \\\;\;\;= {a^2} - ab + {b^2} + 3ab{\left( {a + b} \right)^2}\\\;\;\; = {a^2} - ab + {b^2} + 3ab.1 \\\;\;\;= {a^2} - ab + {b^2} + 3ab = {a^2} + 2ab + {b^2}\\\;\;\; = {\left( {a + b} \right)^2} = 1\end{array}\)

Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại Tuyensinh247.com

 

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Tải về
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store