 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Bài 7. Trường hợp đồng dạng thứ ba
Bài 7. Trường hợp đồng dạng thứ ba
Bài 37 trang 79 SGK Toán 8 tập 2
Hình 44 cho biết
Video hướng dẫn giải
Hình 44 cho biết \(\widehat{EBA} = \widehat{BDC}\).
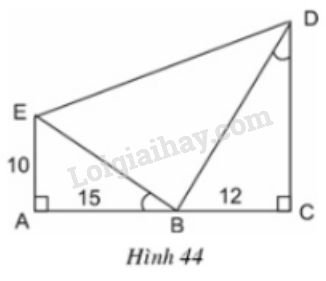
LG a.
Trong hình vẽ, có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.
Phương pháp giải:
Áp dụng: Tam giác có 1 góc vuông là tam giác vuông.
Lời giải chi tiết:
Ta có: \(\widehat{EBA} = \widehat{BDC}\) (giả thiết) mà \(\widehat{BDC} + \widehat{CBD}={90^0}\) (do tam giác BCD vuông tại C)
\( \Rightarrow \widehat{EBA} + \widehat{CBD}={90^0}\)
Vậy \(\widehat{EBD} = {180^0} - (\widehat{EBA}+ \widehat{CBD})\)\(\, = {180^o} - {90^o} = {90^o}\)
Vậy trong hình vẽ có ba tam giác vuông đó là:
\(∆ABE, ∆CBD, ∆EBD.\)
LG b.
Cho biết \(AE = 10cm, AB = 15cm, BC = 12cm\). Hãy tính độ dài các đoạn thẳng \(CD, BE, BD\) và \(ED\) (làm tròn đến chữ số thập phân thứ nhất).
Phương pháp giải:
Áp dụng:
- Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Tính chất hai tam giác đồng dạng.
- Định lí Pitago.
Lời giải chi tiết:
\(∆ABE\) và \(∆CDB\) có:
\(\widehat{A} = \widehat{C}=90^o\)
\(\widehat{ABE}= \widehat{CDB}\) (giả thiết)
\( \Rightarrow ∆ABE ∽ ∆CDB\) (g-g)
\( \Rightarrow \dfrac{AB}{CD} = \dfrac{AE}{CB}\) (tính chất hai tam giác đồng dạng)
\( \Rightarrow CD = \dfrac{AB.CB}{AE} = 18\, (cm)\)
- Áp dụng định lí pitago ta có:
\( ∆ABE\) vuông tại \(A\)
\( \Rightarrow BE = \sqrt{AE^{2}+AB^{2}}\) \(\,=\sqrt{10^{2}+15^{2}}\) \( \approx 18\, (cm)\).
\(∆BCD\) vuông tại \(C\)
\( \Rightarrow BD = \sqrt {B{C^2} + D{C^2}} \) \(= \sqrt {{{12}^2} + {{18}^2}} \approx 21,6\,\,cm\)
\(∆EBD\) vuông tại \(B\)
\( \Rightarrow ED = \sqrt{EB^{2}+BD^{2}}\) \(=\sqrt{325+ 468} \approx 28,2\, (cm)\)
LG c.
So sánh diện tích tam giác \(BDE\) với tổng diện tích hai tam giác \(AEB\) và \(BCD\).
Phương pháp giải:
Sử dụng: Công thức tính diện tích tam giác, diện tích hình thang.
Lời giải chi tiết:
Ta có:
\(S_{ABE} + S_{DBC}\)
\(= \dfrac{1}{2}AE.AB + \dfrac{1}{2}BC.CD\)
\(= \dfrac{1}{2}. 10.15 + \dfrac{1}{2}.12.18\)
\(= 75 + 108 = 183\;cm^2\).
Ta có: \(A{\rm{E}}//DC\,\,\left(\text{ cùng } { \bot AC} \right) \Rightarrow \) \(ACDE\) là hình thang.
\(S_{ACDE} = \dfrac{1}{2}.(AE + CD).AC\)
\(= \dfrac{1}{2}.(10 + 18).27= 378\;cm^2\)
\( \Rightarrow S_{EBD} = S_{ACDE} - (S_{ABE}+ S_{DBC})\)\(\; = 378 - 183 = 195\,cm^2\)
\(S_{EBD}> S_{ABE} + S_{DBC}\) \(( 195 > 183)\).
Cách khác:
Các em có thể thay độ dài BE, BD tính được ở câu b để tính diện tích tam giác EBD.
Loigiaihay.com











