Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 2. Định lí đảo và hệ quả của định lí Ta - let

Trả lời câu hỏi 1 Bài 2 trang 59 SGK Toán 8 Tập 2


Đề bài

Tam giác \(ABC\) có \(AB=6cm\); \(AC=9cm\).

Lấy trên cạnh \(AB\) điểm \(B'\), trên cạnh \(AC\) điểm \(C'\) sao cho \(AB'=2cm\); \(AC'=3cm\) (h8)

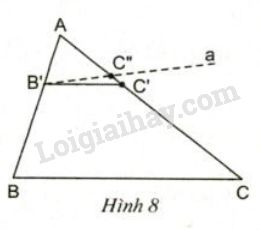
1) So sánh các tỉ số \(\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\).

2) Vẽ đường thẳng \(a\) đi qua \(B'\) và song song với \(BC\), đường thẳng \(a\) cắt \(AC\) tại điểm \(C''\).

a) Tính độ dài đoạn thẳng \(AC''\).

b) Có nhận xét gì về \(C'\) và \(C''\) và về hai đường thẳng \(BC\) và \(B'C'\)?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

1) Tính tỉ số đoạn thẳng rồi so sánh.

2) Sử dụng đinh lí Ta-lét 

Lời giải chi tiết

1)

\(\begin{array}{l}\dfrac{{AB'}}{{AB}} = \dfrac{2}{6} = \dfrac{1}{3}\\\dfrac{{AC'}}{{AC}} = \dfrac{3}{9} = \dfrac{1}{3}\\ \Rightarrow \dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}}\end{array}\)

2)

a) Vì \(B'C''//BC\) , theo định lí Ta-lét ta có:

\(\dfrac{{AB'}}{{AB}} = \dfrac{{AC''}}{{AC}} = \dfrac{1}{3}\)

\( \Rightarrow AC'' = \dfrac{1}{3}AC = \dfrac{1}{3}.9 = 3\,cm\)

b) Ta có: \(AC' = AC'' = 3\,cm \Rightarrow C' \equiv C''\)

Do \(C' \equiv C'' \Rightarrow B'C' \equiv B'C''\)  nên \(B'C'//BC\)

Loigiaihay.com


Bình chọn:
4.7 trên 45 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 8 trên Tuyensinh247.com cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua