Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 6. Phép trừ các phân thức đại số

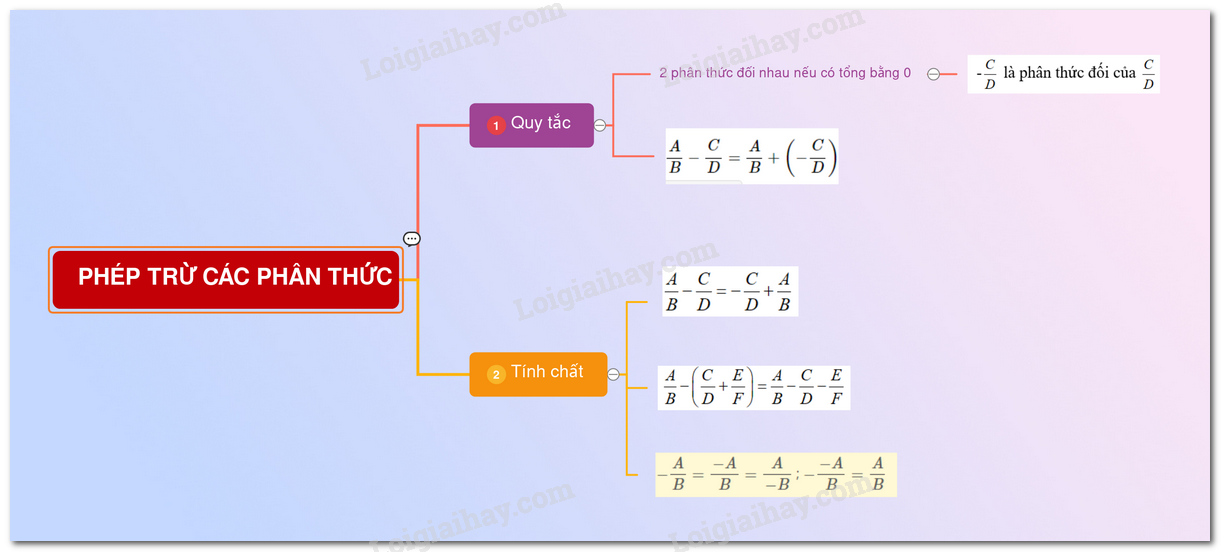
Lý thuyết phép trừ các phân thức đại số


1. Phân thức đối.

1. Phân thức đối

Hai phân thức được gọi là đối nhau nếu tổng của chúng bằng \(0\).

Phân thức đối của phân thức \( \dfrac{A}{B}\) được kí hiệu là \( -\dfrac{A}{B}\)

Vậy \( -\dfrac{A}{B} =\dfrac{-A}{B}\) và \( -\dfrac{-A}{B}=\dfrac{A}{B}\)

Ví dụ: \(\dfrac{x}{x-2}\) là phân thức đối của phân thức \(\dfrac{-x}{x-2}\)

2. Phép trừ

Quy tắc: Muốn trừ phân thức \( \dfrac{A}{B}\) cho phân thức \( \dfrac{C}{D}\), ta cộng \( \dfrac{A}{B}\) với phân thức đối của \( \dfrac{C}{D}\)

Vậy: \( \dfrac{A}{B}-\dfrac{C}{D}=\dfrac{A}{B}+\left( { - \dfrac{C}{D}} \right)\).

Ví dụ: 

\( \dfrac{4x-1}{3x^{2}y}-\dfrac{7x-1}{3x^{2}y}\) \( =\dfrac{4x-1}{3x^{2}y}+\dfrac{-(7x-1)}{3x^{2}y}\)

\( =\dfrac{4x-1-7x+1}{3x^{2}y}\) \( =\dfrac{-3x}{3x^{2}y}=-\dfrac{1}{xy}\). 


Bình chọn:
4.3 trên 44 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 8 trên Tuyensinh247.com cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua