Lý thuyết định lí đảo và hệ quả của định lí Talet

1. Định lí Ta-lét đảo

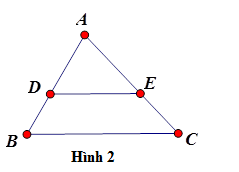
Ví dụ: $\Delta ABC$có \(\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}} \Rightarrow DE{\rm{//}}BC\) (h.2)

2. Hệ quả của định lí Ta-lét

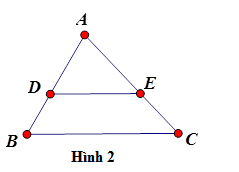
\(\Delta ABC,DE//BC \)\(\Rightarrow \dfrac{{AD}}{{AB}}= \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}}\) (h.2)

Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng \(a\) song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.

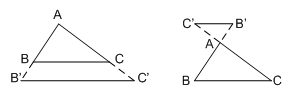
Ở hai hình trên \(\Delta ABC\) có \(BC{\rm{//}}B'C'\)\( \Rightarrow \dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}} = \dfrac{{B'C'}}{{BC}}.\)

3. Các dạng toán thường gặp

Dạng 1: Tính độ dài đoạn thẳng, chu vi, diện tích và các tỉ số.

Phương pháp:

Sử dụng định lí Ta-lét, hệ quả định lí Ta-lét, tỉ số đoạn thẳng để tính toán.

+ Định lý: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

+ Hệ quả: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.

+ Ngoài ra, ta còn sử dụng đến tính chất tỉ lệ thức:

Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\)thì \( \left\{ \begin{array}{l}ad = bc\\\dfrac{a}{c} = \dfrac{b}{d}\\\dfrac{{a + b}}{b} = \dfrac{{c + d}}{d};\,\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\\\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}} = \dfrac{{a - c}}{{b - d}}\end{array} \right.\)

Dạng 2: Chứng minh hai đường thẳng song song, chứng minh các đẳng thức hình học.

Phương pháp:

Ta sử dụng định lí Ta-lét, định lí đảo và hệ quả để chứng minh.

4. Bài tập về định lí đảo và hệ quả của định lí Talet

Bài 1. Hãy chọn câu sai. Cho hình vẽ với $AB<AC$: 

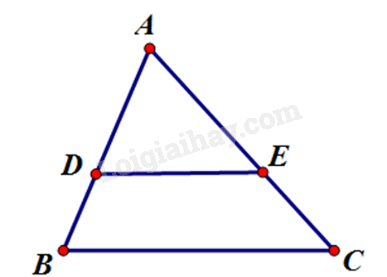
A. \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} \Rightarrow DE//BC\).

B. \(\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}} \Rightarrow DE//BC\).

C. \(\dfrac{{AB}}{{DB}} = \dfrac{{AC}}{{EC}} \Rightarrow DE//BC\).

D. \(\dfrac{{AD}}{{DE}} = \dfrac{{AE}}{{ED}} \Rightarrow DE//BC\).

Lời giải: Theo định lý đảo của định lý Ta-lét: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Nên D sai.

Chọn đáp án D.

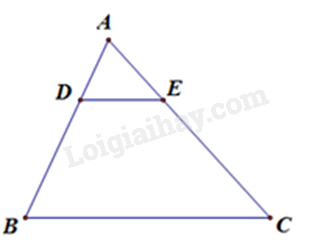
Bài 2. Cho hình vẽ, trong đó $DE{\rm{//}}BC$, $AD = 12,\,\,DB = 18,\,\,CE = 30$. Độ dài $AC$ bằng:

A. \(20\)                      

B. \(\dfrac{{18}}{{25}}\)                     

C. \(50\)                      

D. \(45\)

Lời giải: Vì $DE{\rm{//}}BC$, theo định lý Ta-lét ta có \(\dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{EC}} \Leftrightarrow \dfrac{{12}}{{18}} = \dfrac{{AE}}{{30}}\)\( \Rightarrow EA = \dfrac{{30.12}}{{18}} = 20\,cm\)

Nên \(AC = AE + EC = 50\,cm\)

Chọn đáp án C.

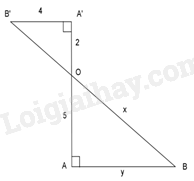
Bài 3. Tính các độ dài $x,y$ trong hình bên:

A. \(x = 2\sqrt 5 ,\;y = 10\)

B. \(x = 10\sqrt 5 ,\;y = 9\)

C. \(x = 6\sqrt 5 ,\;y = 10\)        

D. \(x = 5\sqrt 5 ,\;y = 10\)\(\)

Lời giải: Áp dụng định lý Py-ta-go cho tam giác vuông \(OA'B'\), ta có:

\(\begin{array}{l}OA{'^2} + A'B{'^2} = OB{'^2}\\ \Leftrightarrow {2^2} + {4^2} = OB{'^2}\\ \Leftrightarrow OB{'^2} = 20\\ \Rightarrow OB' = \sqrt {20} \end{array}\)

\(A'B' \bot AA',\;AB \bot AA' \Rightarrow A'B'\parallel AB\) (Theo định lý từ vuông góc đến song song)

Áp dụng định lý Ta-let, ta có:

\(\dfrac{{OA'}}{{OA}} = \dfrac{{OB'}}{{OB}} = \dfrac{{A'B'}}{{AB}}\)

\( \Rightarrow \left\{ \begin{array}{l}\dfrac{{\sqrt {20} }}{x} = \dfrac{2}{5}\\\dfrac{4}{y} = \dfrac{2}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{5.\sqrt {20} }}{2} = 5\sqrt 5 \\y = \dfrac{{4.5}}{2} = 10\end{array} \right.\)

Vậy \(x = 5\sqrt 5 \) và \(y = 10\).

Chọn đáp án D.

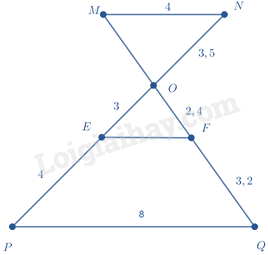
Bài 4. Cho hình vẽ sau. Có bao nhiêu cặp đường thẳng song song?

A. 0

B. 1

C. 2

D. 3

Lời giải: Ta có: \(\frac{{MN}}{{PQ}} = \frac{4}{8} = \frac{1}{2};\frac{{ON}}{{OP}} = \frac{{3,5}}{{3 + 4}} = \frac{1}{2} \Rightarrow \frac{{MN}}{{PQ}} = \frac{{ON}}{{OP}}\)

\( \Leftrightarrow MN // PQ\) (định lý Thalès đảo) (1)

Ta có: \(\frac{{OE}}{{PE}} = \frac{3}{4};\frac{{OF}}{{FQ}} = \frac{{2,4}}{{3,2}} = \frac{3}{4} \Rightarrow \frac{{OE}}{{PE}} = \frac{{OF}}{{FQ}}\)

\( \Rightarrow EF // PQ\) (định lý Thalès đảo) (2)

Từ (1), (2) \( \Rightarrow MN // EF\) (cùng song song với \(PQ\) ).

Vậy có 3 cặp đường thẳng song song.

Chọn đáp án D.

Bài 5. Cho tứ giác \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Đường thẳng qua \(A\) và song song với \(BC\) cắt \(BD\) ở \(E\) . Đường thẳng qua \(B\) song song với \(AD\) cắt \(AC\) ở \(F\) . Chọn kết luận sai?

A. \(\frac{{OE}}{{OB}} = \frac{{OA}}{{OC}}\)

B. \(\frac{{EF}}{{AB}} = \frac{{OE}}{{OB}}\)

C. \(\frac{{OB}}{{OD}} = \frac{{OF}}{{OA}}\)

D. \(\frac{{OE}}{{OD}} = \frac{{OF}}{{OC}}\)

Lời giải:

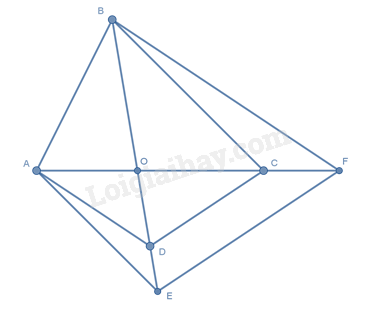
\(AE // BC\) nên theo hệ quả của định lí Thalès ta có: \(\frac{{OE}}{{OB}} = \frac{{OA}}{{OC}}\) (1)

\(BF // AD\) nên theo hệ quả của định lí Thalès ta có: \(\frac{{OB}}{{OD}} = \frac{{OF}}{{OA}}\) (2)
Từ (1), (2) \( \Rightarrow \frac{{OE}}{{OB}} \cdot \frac{{OB}}{{OD}} = \frac{{OA}}{{OC}} \cdot \frac{{OF}}{{OA}}\) hay \(\frac{{OE}}{{OD}} = \frac{{OF}}{{OC}}\)

Chọn đáp án B.