Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Ôn tập chương II: Đa giác. Diện tích đa giác

Bài 42 trang 132 SGK Toán 8 tập 1


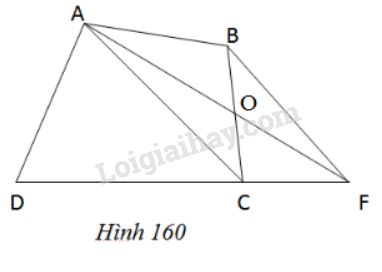
Trên hình 160 (AC//BF), hãy tìm tam giác có diện tích bằng diện tích của tứ giác ABCD.

Đề bài

Trên hình \(160\) \((AC//BF)\), hãy tìm tam giác có diện tích bằng diện tích của tứ giác \(ABCD\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Áp dụng cách tính diện tích tam giác, tứ giác.

Lời giải chi tiết

Gọi \(O\) là giao điểm của \(AF\) và \(BC\).

Ta có \(\Delta A{\rm{D}}F\) có diện tích bằng diện tích tứ giác \(ABCD\).

Thật vậy, do \( AC// BF\) nên  \({S_{ABC}} = {S_{AFC}}\) vì có cùng đáy \(AC\) và cùng chiều cao là khoảng cách giữa hai đường thẳng song song \(AC, BF.\)

Ta có:  \({S_{ABC}} = {S_{AFC}}\) (chứng minh trên)

\( \Rightarrow {S_{ABO}} + {S_{ACO}} = {S_{CF{\rm{O}}}} + {S_{AC{\rm{O}}}}\)

\(\Rightarrow {S_{ABO}} = {S_{CFO}}\).

Do đó  \({S_{ADF}} = {S_{AOCD}} + {S_{CFO}} \)\(= {S_{AOCD}} + {S_{ABO}}= {S_{ABCD}}\)

Vậy  \({S_{ADF}} = {S_{ABCD}}\)

Loigiaihay.com


Bình chọn:
4.3 trên 78 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store