 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Bài 3. Tính chất đường phân giác của tam giác
Bài 3. Tính chất đường phân giác của tam giác
Bài 21 trang 68 SGK Toán 8 tập 2
Cho tam giác ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích tam giác ADM, biết AB= m, AC= n( n>m). Và diện tích của tam giác ABC là S.
Đề bài
a) Cho tam giác \(ABC\) với đường trung tuyến \(AM\) và đường phân giác \(AD\). Tính diện tích tam giác \(ADM\), biết \(AB= m, AC= n\;( n>m)\) và diện tích của tam giác \(ABC\) là \(S\).
b) Cho \(n = 7cm, m = 3cm\). Hỏi diện tích tam giác \(ADM\) chiếm bao nhiêu phần trăm diện tích tam giác \(ABC\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Tính chất đường phân giác trong tam giác. Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Lời giải chi tiết
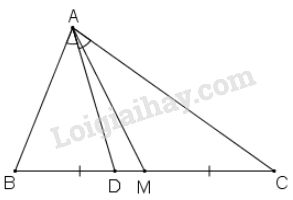
a) Ta có \(AD\) là đường phân giác của \(∆ABC\) (gt) nên
\(\dfrac{{B{\rm{D}}}}{{DC}} = \dfrac{{AB}}{{AC}}\) (Tính chất đường phân giác của tam giác)
\(\dfrac{S_{ABD}}{S_{ADC}} = \dfrac{DB}{DC}\) (do hai tam giác có chung chiều cao từ đỉnh A)
Nên \(\dfrac{S_{ABD}}{S_{ADC}} = \dfrac{DB}{DC}= \dfrac{AB}{AC}= \dfrac{m}{n}\)
\(\eqalign{
& \Rightarrow {{{S_{ADC}}} \over {{S_{ABD}}}} = {n \over m} \cr
& \Rightarrow {{{S_{ADC}}} \over {{S_{ABD}}}} + 1 = {n \over m} + 1 \cr
& \Rightarrow {{{S_{ADC}} + {S_{ABD}}} \over {{S_{ABD}}}} = {{n + m} \over m} \cr} \)
\( \Rightarrow \dfrac{S_{ABD}}{S_{ADC}+S_{ABD}}= \dfrac{m}{n+m}\)
hay \(\dfrac{S_{ABD}}{S_{ABC}}= \dfrac{m}{n+m}\)
\( \Rightarrow {S_{AB{\rm{D}}}} = \dfrac{{mS}}{{n + m}}\)
Vì \(AM\) là trung tuyến của \(∆ABC\) (gt) \(\Rightarrow S_{ABM}= \dfrac{1}{2}S_{ABC}\).
Có \(AB < AC( m<n)\) và \(AD\) là đường phân giác, \(AM\) là đường trung tuyến kẻ từ \(A\) nên \(AD\) nằm giữa \(AB\) và \(AM\).
\( \Rightarrow S_{ADM}= S_{ABM}- S_{ABD}\)
\( \Rightarrow S_{ADM} = \dfrac{1}{2}S -\dfrac{m}{n+m}S \)\(\,= \dfrac{S(m+n-2m)}{2(m+n)}\)
\(S_{ADM}= \dfrac{S(n -m)}{2(m+n)}\) (với \(n>m\))
b) Khi \(n = 7cm, m = 3cm\) ta có:
\({S_{A{\rm{D}}M}} = \dfrac{{7 - 3}}{{2\left( {7 + 3} \right)}}.S = \dfrac{S}{5} = \dfrac{{20.S }}{100} \)\(\,= 20\% S\)
Vậy \(S_{ADM} = 20\%S_{ABC}\).
Loigiaihay.com












Danh sách bình luận