 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Bài 3. Tính chất đường phân giác của tam giác
Bài 3. Tính chất đường phân giác của tam giác
Bài 16 trang 67 SGK Toán 8 tập 2
Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng
Đề bài
Tam giác \(ABC\) có độ dài các cạnh \(AB= m, AC= n\) và \(AD\) là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác \(ABD\) và diện tích tam giác \(ACD\) bằng \(\dfrac{m}{n}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Công thức tính diện tích của tam giác, tính chất đường phân giác của tam giác.
Lời giải chi tiết
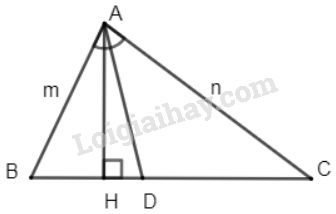
Kẻ \(AH ⊥ BC\)
Ta có:
\({S_{ABD}} = \dfrac{1}{2}AH.BD\)
\({S_{ACD}} = \dfrac{1}{2}AH.DC\)
\( \Rightarrow \dfrac{S_{ABD}}{S_{ACD}} = \dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.DC} = \dfrac{BD}{DC}\)
Mặt khác: \(AD\) là đường phân giác của \(∆ABC\) (gt)
\( \Rightarrow \dfrac{BD}{DC}= \dfrac{AB}{AC} = \dfrac{m}{n}\) (tính chất đường phân giác của tam giác)
Vậy \(\dfrac{S_{ABD}}{S_{ACD}} = \dfrac{m}{n}\) (điều phải chứng minh).
Loigiaihay.com












Danh sách bình luận