Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 2. Tính chất cơ bản của phân thức

Lý thuyết tính chất cơ bản của phân thức


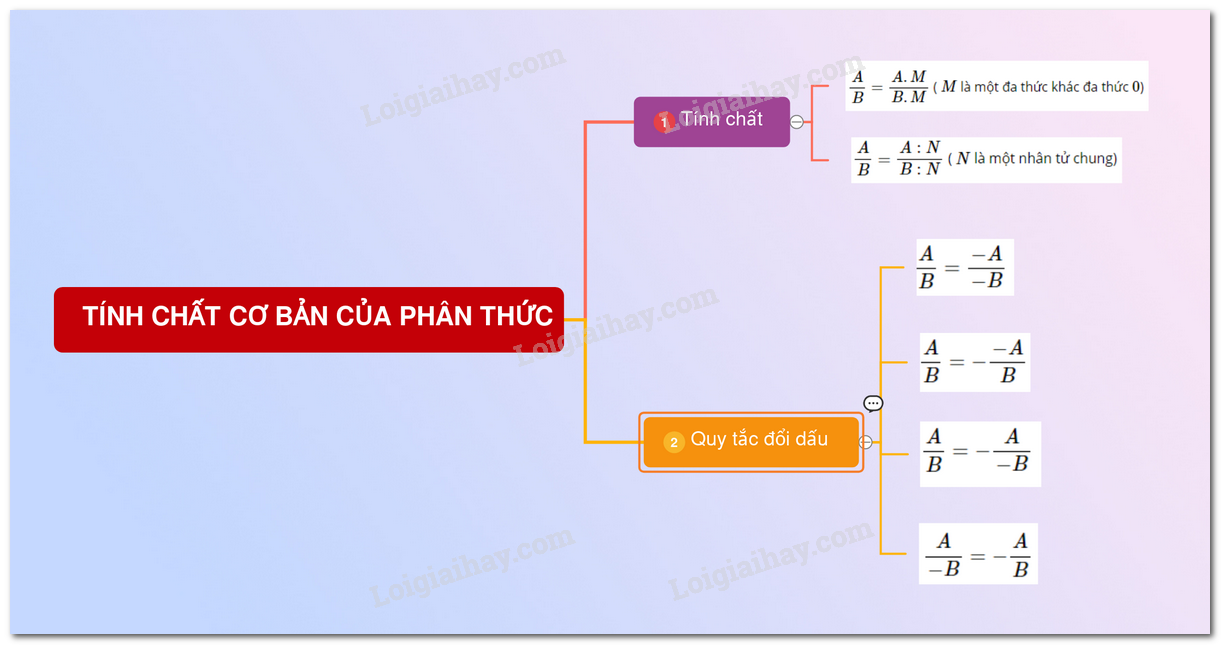
1.Tính chất

1. Tính chất cơ bản của phân thức

- Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

\( \dfrac{A}{B}= \dfrac{A.M}{B.M}\) ( \(M\) là một đa thức khác đa thức \(0\))

- Nếu chia cả tử và mẫu của một đa thức cho một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.

\( \dfrac{A}{B}= \dfrac{A : N}{B : N}\) ( \(N\) là một nhân tử chung)

Ví dụ: 

\(\begin{array}{l}
\dfrac{x}{{x + 1}} = \dfrac{{x.2x}}{{\left( {x + 1} \right).2x}} = \dfrac{{2{x^2}}}{{2{x^2} + 2x}}\\
\dfrac{{15{x^2}}}{{3x\left( {2x + 1} \right)}} = \dfrac{{15{x^2}:3x}}{{3x\left( {2x + 1} \right):3x}} = \dfrac{{5x}}{{2x + 1}}
\end{array}\)

2. Qui tắc đổi dấu

 Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.

\( \dfrac{A}{B}= \dfrac{-A}{-B}\)

Ví dụ: \(\dfrac{{3x}}{4} = \dfrac{{ - 3x}}{{ - 4}}\)


Bình chọn:
4.6 trên 64 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 trên Tuyensinh247.com cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua