Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 1. Một số hệ thức về cạnh và đường cao trong tam gi..

Bài 19 trang 105 SBT toán 9 tập 1


Giải bài 19 trang 105 sách bài tập toán 9. Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN.

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(AB = 6\)cm và \(AC = 8\)cm. Các đường phân giác trong và ngoài của góc \(B\) cắt đường thẳng \(AC\) lần lượt tại \(M\) và \(N\). Tính các đoạn thẳng \(AM\) và \(AN\).   

Phương pháp giải - Xem chi tiết

+ Tính chất đường phân giác:

- Đường phân giác trong của một tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy. 

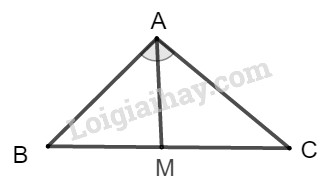
Xét tam giác ABC có AM là phân giác của góc trong \(\widehat {BAC}\).

Ta có hệ thức: \(\dfrac{{AB}}{{AC}} = \dfrac{{AM}}{{MC}}\)

 - Đường phân giác ngoài tại một đỉnh của tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.

+ Tính chất tỉ lệ thức:

\(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}.\) 

Lời giải chi tiết

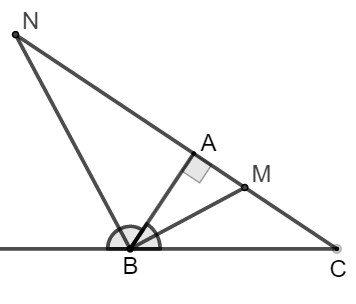
Vì \(BM\) là đường phân giác của góc \(B\) nên ta có:  

\(\dfrac{{MA}}{{MC}} = \dfrac{{AB}}{{BC}}\)\( \Rightarrow \dfrac{{MA}}{{MA + MC}} = \dfrac{{AB}}{{AB + BC}}\) (tính chất tỉ lệ thức)

Suy ra: \(MA = \dfrac{{AB.(MA + MC)}}{{AB + BC}}\)\(= \dfrac{{AB.AC}}{{AB + BC}}\)\( = \dfrac{{6.8}}{{6 + 10}} = \dfrac{{48}}{{16}} = 3\left( {cm} \right)\)

Vì \(BM, BN\) lần lượt là đường phân giác của góc  trong và góc ngoài tại đỉnh \(B\) nên ta có: \(BM \bot BN\)

Suy ra tam giác \(BMN\) vuông tại \(B\). 

Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có: \(A{B^2} = AM.AN\)

 Suy ra: \(AN = \dfrac{{A{B^2}}}{{AM}} = \dfrac{{{6^2}}}{ 3} = \dfrac{{36}}{ 3} = 12\left( {cm} \right)\)

Loigiaihay.com


Bình chọn:
4.5 trên 23 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store