Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 1. Một số hệ thức về cạnh và đường cao trong tam gi..

Bài 11 trang 104 SBT toán 9 tập 1


Giải bài 11 trang 104 sách bài tập toán 9. Cho tam giác ABC vuông tại A. Biết AB/AC=5/6; đường cao AH = 30. Tính HB,HC.

Đề bài

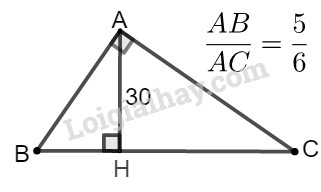
Cho tam giác ABC vuông tại A. Biết rằng \(\dfrac{{AB} }{{AC}} = \dfrac{5}{6}\), đường cao \(AH = 30cm\). Tính \(HB, HC\).

Phương pháp giải - Xem chi tiết

Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\).

Khi đó ta có các hệ thức sau: 

+) \(A{B^2} = BH.BC\) 

+) \(A{C^2} = CH.BC\) 

+) \(AH^2=HB.HC;AB.AC=AH.BC\)

+) \(AB^2+AC^2=BC^2\) (định lý Pytago).

Lời giải chi tiết

Xét hai tam giác vuông \(AHB\) và \(CHA,\) ta có:

\(\widehat {AHB} = \widehat {CHA} = {90^0}\) 

\(\widehat {ABH} = \widehat {CAH}\) (hai góc cùng phụ \(\widehat {ACB}\)) 

Vậy \( ∆AHB \backsim ∆CHA\) (g.g)

Suy ra: \(\dfrac{{AH}}{{HC}} = \dfrac{{AB}}{{CA}}.\)  (1)

Theo đề bài: \(\dfrac{{AB}}{{AC}} = \dfrac{5}{6}\) và \(AH = 30(cm)\)  (2)

Từ (1) và (2) suy ra: \(\dfrac{{30}}{{HC}} = \dfrac{5 }{6} \Rightarrow HC = \dfrac{{30.6}}{5} = 36(cm)\)

Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:

\(A{H^2} = HB.HC \)\(\Rightarrow HB = \dfrac{{A{H^2}}}{{HC}} = \dfrac{{{{30}^2}}}{{36}} = 25(cm)\)

Loigiaihay.com


Bình chọn:
4.7 trên 26 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store