 Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học
 Ôn tập chương I: Phép nhân và phép chia các đa thức
Ôn tập chương I: Phép nhân và phép chia các đa thức
Đề kiểm tra 45 phút ( 1 tiết) - Đề số 5 - Chương 1 - Đại số 8
Giải Đề kiểm tra 45 phút ( 1 tiết) - Đề số 5 - Chương 1 - Đại số 8
Đề bài
Bài 1. Rút gọn biểu thức :
a) \(A = \left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 2} \right) \)\(- 2\left( {x - 1} \right).\)
b) \(B = {\left( {x - 2y} \right)^2} + {\left( {x + 2y} \right)^2}\)\( + \left( {4y + 1} \right)\left( {1 - 4y} \right).\)
Bài 2. Phân tích các đa thức sau thành nhân tử:
a) \({\left( {2x + 3} \right)^2} - \left( {{x^2} - 6x + 9} \right)\)
b) \({x^2} - 4{y^2} + 4x + 8y.\)
Bài 3. Tìm m để đa thức \(A\left( x \right) = 2{x^3} - 7{x^2} + 5x + m\) chia hết cho đa thức \(B(x) = 2x - 3.\)
Bài 4. Tìm x, biết: \({x^2} - 3x + 5\left( {x - 3} \right) = 0.\)
Bài 5. Tìm giá trị lớn nhất của biểu thức: \(P = - {x^2} - {y^2} + 4x - 4y + 2.\)
LG bài 1
Phương pháp giải:
Sử dụng qui tắc nhân đơn thức với đa thức, đa thức với đa thức và các hằng đẳng thức:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
{\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\\
{\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}
\end{array}\\
{{a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)}
\end{array}\)
\({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\)
Lời giải chi tiết:
a) \(A = \left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - x\left( {{x^2} - 2} \right) \)\(- 2\left( {x - 1} \right)\)
\(= {x^3} - 27 - {x^3} + 2x - 2x + 2\)\(\; = - 25.\)
b) \(B = {\left( {x - 2y} \right)^2} + {\left( {x + 2y} \right)^2}\)\( + \left( {4y + 1} \right)\left( {1 - 4y} \right)\)
\( = {x^2} - 4xy + 4{y^2}+x^2 + 4xy + 4{y^2} + 1 - 16{y^2} \)
\(= 2{x^2} - 8{y^2} + 1.\)
LG bài 2
Phương pháp giải:
Phối hợp nhiều phương pháp để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
a) \({\left( {2x + 3} \right)^2} - \left( {{x^2} - 6x + 9} \right) \)
\(= {\left( {2x + 3} \right)^2} - {\left( {x - 3} \right)^2}\)
\( = \left( {2x + 3 + x - 3} \right)\left( {2x + 3 - x + 3} \right) \)
\(= 3x\left( {x + 6} \right).\)
b) \({x^2} - 4{y^2} + 4x + 8y\)
\(= \left( {x - 2y} \right)\left( {x + 2y} \right) + 4\left( {x + 2y} \right)\)
\(=\left( {x + 2y} \right)\left( {x - 2y + 4} \right).\)
LG bài 3
Phương pháp giải:
Phép chia hết có số dư bằng 0
Lời giải chi tiết:
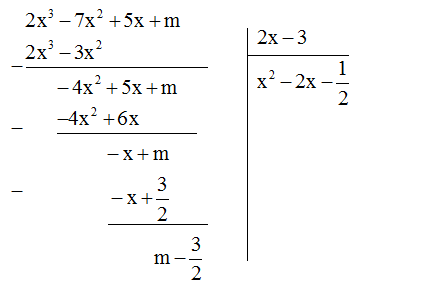
A(x) chia hết cho B(x) khi \(m - {3 \over 2} = 0 \Rightarrow m = {3 \over 2}.\)
LG bài 4
Phương pháp giải:
Đưa về dạng \(A\left( x \right).B\left( x \right) = 0 \)\(\Rightarrow A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\)
Lời giải chi tiết:
Ta có:
\({x^2} - 3x + 5\left( {x - 3} \right) \)
\(= x\left( {x - 3} \right) + 5\left( {x - 3} \right) \)
\(= \left( {x - 3} \right)\left( {x + 5} \right).\)
Nên \({x^2} - 3x + 5\left( {x - 3} \right) = 0\)
\(\Rightarrow \left( {x - 3} \right)\left( {x + 5} \right) = 0\)
\(\Rightarrow x - 3 = 0\) hoặc \(x + 5 = 0\)
\( \Rightarrow x = 3\) hoặc \(x = - 5.\)
LG bài 5
Phương pháp giải:
Sử dụng: \(m - {\left( {x - a} \right)^2} - {\left( {y + b} \right)^2} \le m\) với mọi \(x;y\).
Lời giải chi tiết:
Ta có:
\(P = - {x^2} - {y^2} + 4x - 4y + 2.\)
\(= - {x^2} + 4x - 4 - {y^2} - 4y - 4 + 10\)
\( = 10 - \left( {{x^2} - 4x + 4} \right) - \left( {{y^2} + 4y + 4} \right)\)
\(=10 - {\left( {x - 2} \right)^2} - {\left( {y + 2} \right)^2} \le 10\) vì \({\left( {x - 2} \right)^2} \ge 0;\left( {y + 2}\right)^2 \ge 0 \) với mọi x, y.
Vậy giá trị lớn nhất của P bằng 10.
Dấu "=" xảy ra khi \(x - 2 = 0\) và \(y + 2 = 0 \Rightarrow x = 2\) và \(y = - 2.\)
Loigiaihay.com
- Đề kiểm tra 45 phút ( 1 tiết) - Đề số 4 - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Đề số 3 - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Đề số 2 - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Đề số 1 - Chương 1 - Đại số 8
- Lý thuyết Ôn tập chương 1. Phép nhân và phép chia các đa thức
>> Xem thêm












Danh sách bình luận