Đề kiểm tra 15 phút - Đề số 2 - Bài 4 - Chương 2 - Hình học 8
Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 4 - Chương 2 - Hình học 8
Đề bài
Chứng minh rằng: Đường thẳng đi qua trung điểm của đường trung bình và cắt hai đáy của hình thang thì chia hình thang thành hai đa giác có diện tích bằng nhau.
Phương pháp giải - Xem chi tiết
Sử dụng:
Đường trung bình của hình thang bằng nửa tổng hai đáy
Diện tích hình thang bằng nửa tích chiều cao với tổng hai đáy
Lời giải chi tiết
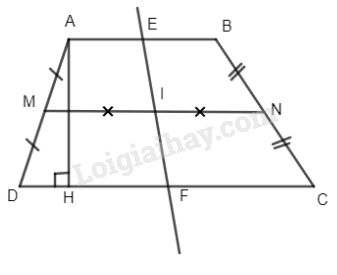
Gọi I là trung điểm của đường trung bình MN và đường thẳng EF đi qua I. Khi đó các tứ giác AEFD, BEFC cũng là các hình thang nên:
\({S_{AEFD}} = {{\left( {AE + DF} \right).AH} \over 2} = MI.AH\)
(tính chất đường trung bình bằng nửa tổng hai cạnh đáy)
Tương tự \({S_{BEFC}} = {{\left( {BE + CF} \right).AH} \over 2} = NI.AI\)
Mà MI = NI (gt)
\( \Rightarrow {S_{AEFD}} = {S_{BEFC}}.\)
Loigiai hay.com













Danh sách bình luận