-
PHẦN ĐẠI SỐ - TOÁN 8 TẬP 1
-
CHƯƠNG I. PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3. Những hằng đẳng thức đáng nhớ
- Bài 4. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 5. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Ôn tập chương I: Phép nhân và phép chia các đa thức
- Đề kiểm tra 15 phút - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Đại số 8
-
CHƯƠNG II. PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Ôn tập chương II: Phân thức đại số
- Đề kiểm tra 15 phút – Chương 2 – Đại số 8
- Đề kiểm tra 45 phút (1 tiết ) – Chương 2 – Đại số 8
-
-
PHẦN HÌNH HỌC - TOÁN 8 TẬP 1
-
CHƯƠNG I. TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương I: Tứ giác
- Đề kiểm tra 15 phút - Chương 1 - Hình học 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 8
-
CHƯƠNG II. ĐA GIÁC, DIỆN TÍCH ĐA GIÁC
- Bài 1. Đa giác. Đa giác đều
- Bài 2. Diện tích hình chữ nhật
- Bài 3. Diện tích tam giác
- Bài 4. Diện tích hình thang
- Bài 5. Diện tích hình thoi
- Bài 6. Diện tích đa giác
- Ôn tập chương II: Đa giác. Diện tích đa giác
- Đề kiểm tra 15 phút - Chương 2 - Hình học 8
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 8
-
-
Đề cương ôn tập học kì 1 toán 8
-
Đề thi học kì 1 mới nhất có lời giải
-
PHẦN ĐẠI SỐ - TOÁN 8 TẬP 2
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
- Bài 1. Mở đầu về phương trình
- Bài 2. Phương trình bậc nhất một ẩn và cách giải
- Bài 3. Phương trình đưa được về dạng ax + b = 0
- Bài 4. Phương trình tích
- Bài 5. Phương trình chứa ẩn ở mẫu
- Bài 6. Giải bài toán bằng cách lập phương trình
- Bài 7. Giải bài toán bằng cách lập phương trình (tiếp)
- Ôn tập chương III: Phương trình bậc nhất một ẩn
-
CHƯƠNG IV. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
-
PHẦN HÌNH HỌC - TOÁN 8 TẬP 2
-
CHƯƠNG III. TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta - let trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta - let
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất
- Bài 6. Trường hợp đồng dạng thứ hai
- Bài 7. Trường hợp đồng dạng thứ ba
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Bài 9. Ứng dụng thực tế của tam giác đồng dạng
- Ôn tập chương III: Tam giác đồng dạng
-
CHƯƠNG IV. HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương IV: Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM - TOÁN 8
-
-
Đề thi học kì 2 mới nhất có lời giải
-
Đề cương ôn tập học kì 2
-
Câu hỏi tự luyện Toán 8
-
Tải 30 đề kiểm tra giữa kì 1 Toán 8
-
Tải 30 đề ôn tập kiểm tra học kì 1 Toán 8
-
Tải 30 đề thi học kì 1 của các trường Toán 8
-
Tải 30 đề kiểm tra giữa kì 2 Toán 8
-
Tải 30 đề ôn tập học kì 2 Toán 8
-
Tải 30 đề thi học kì 2 của các trường Toán 8
Bài 81 trang 108 SGK Toán 8 tập 1
Cho hình 106. Tứ giác AEDF là hình gì ? Vì sao ?
Đề bài
Cho hình \(106.\) Tứ giác \(AEDF\) là hình gì ? Vì sao ?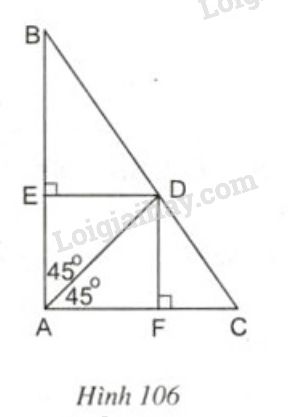 
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng dấu hiệu nhận biết hình vuông: Hình thoi có một góc vuông là hình vuông.
Lời giải chi tiết
Cách 1:
Ta có: \(\widehat {EAF} = \widehat {EAD} + \widehat {DAF} = {45^0} + {45^0} \)\(= {90^0}\)
Tứ giác AEDF có 3 góc vuông nên là hình chữ nhật
Mà đường chéo \(AD\) là phân giác của góc \(A\)
Vậy AEDF là hình vuông ( Dấu hiệu nhận biết hình vuông)
Cách 2:
Tứ giác \(AEDF\) có \(EA // DF\) (cùng vuông góc \(AC\))
\(DE // FA\) (cùng vuông góc với \(AB\))
Suy ra \(AEDF\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
Hình bình hành \(AEDF\) có đường chéo \(AD\) là phân giác của góc \(A\) (giả thiết) nên là hình thoi (dấu hiệu nhận biết hình thoi)
Hình thoi \(AEDF\) có \(\widehat {EAF} = \widehat {EAD} + \widehat {DAF} = {45^0} + {45^0} \)\(= {90^0}\)
\(\Rightarrow \) Hình thoi \(AEDF\) có \(1\) góc vuông nên là hình vuông (dấu hiệu nhận biết hình vuông)
Cách 3:
Tứ giác \(AEDF\) có \(EA // DF\) (cùng vuông góc \(AC\))
\(DE // FA\) (cùng vuông góc với \(AB\))
Suy ra \(AEDF\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
Hình bình hành \(AEDF\) có \(\widehat {EAF} = \widehat {EAD} + \widehat {DAF} = {45^0} + {45^0} \)\(= {90^0}\) nên \(AEDF\) là hình chữ nhật.
Hình chữ nhật \(AEDF\) có đường chéo \(AD\) là phân giác của góc \(A\) nên \(AEDF\) là hình vuông.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 82 trang 108 SGK Toán 8 tập 1
- Bài 83 trang 109 SGK Toán 8 tập 1
- Bài 84 trang 109 SGK Toán 8 tập 1
- Bài 85 trang 109 SGK Toán 8 tập 1
- Bài 86 trang 109 SGK Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
