Bài 47 trang 84 SGK Toán 8 tập 2

Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là 54

Đề bài

Tam giác ABC có độ dài các cạnh là \(3cm, 4cm, 5cm\). Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là \(54c{m^2}\)

Tính độ dài các cạnh của tam giác \(A'B'C'\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Áp dụng tính chất của hai tam giác đồng dạng, công thức tính diện tích tam giác.

Lời giải chi tiết

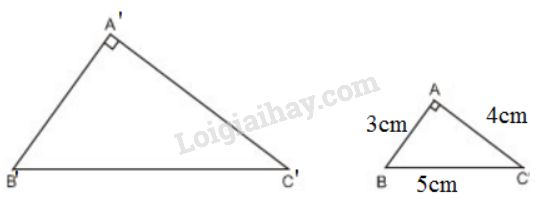
Xét \(∆ABC\) có \(AB=3cm,AC=4cm,BC=5cm\).

Ta có:

\({3^2} + {4^2} = 25 = {5^2} \Rightarrow \Delta ABC\) vuông tại \(A\) (định lí Pitago đảo)

Nên \({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.4 = 6c{m^2}\)

Vì \(∆ABC ∽ ∆A'B'C'\) (gt)

\(\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AC}}{{A'C'}}\) (tính chất hai tam giác đồng dạng)

\( \Rightarrow \dfrac{S_{ABC}}{S_{A'B'C'}} = {\left( {\dfrac{{AB}}{{A'B'}}} \right)^2}\) (tỉ số diện tích bằng bình phương tỉ số đồng dạng)

Do đó: \( \dfrac{6}{54} = {\left( {\dfrac{{AB}}{{A'B'}}} \right)^2}\)

\(\eqalign{
& \Rightarrow {\left( {{{AB} \over {A'B'}}} \right)^2} = {1 \over 9} \cr
& \Rightarrow {{AB} \over {A'B'}} = {1 \over 3} \cr
& \Rightarrow A'B' = 3AB = 3.3 = 9cm \cr} \)

Tức là độ dài mỗi cạnh của tam giác \(A'B'C'\) gấp \(3\) lần độ dài mỗi cạnh của cạnh của tam giác \(ABC\).

Vậy ba cạnh của tam giác \(A'B'C'\) là \(A'B'=9cm,A'C'= 12cm, \)\(\,B'C'=15cm\).

Loigiaihay.com

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.4 trên 285 phiếu

Bài tiếp theo

Bài 48 trang 84 SGK Toán 8 tập 2
Bóng của một cột điện trên mặt đất có độ dài là 4.5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m.
Bài 49 trang 84 SGK Toán 8 tập 2
Ở hình 51, tam giác ABC vuông tại A có đường cao AH
Bài 50 trang 84 SGK Toán 8 tập 2
Bóng của một ống khói nhà máy trên mặt đất có độ dài 36,9m. Cùng thời điểm đó, một thanh sắt cao 2,1 m cắm vuông góc với mặt đất có bóng dài 1,62m.
Bài 51 trang 84 SGK Toán 8 tập 2
Giải bài 51 trang 84 SGK Toán 8 tập 2. Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó(h.53)
Bài 52 trang 85 SGK Toán 8 tập 2
Cho một tam giác vuông, trong đó có cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.
Bài 46 trang 84 SGK Toán 8 tập 2
Giải bài 46 trang 84 SGK Toán 8 tập 2. Trên hình 50, hãy chỉ ra các tam giác đồng dạng. Viết các tam giác này theo thứ tự đỉnh tương ứng và giải thích vì sao chúng đồng dạng?
Trả lời câu hỏi Bài 8 trang 81 SGK Toán 8 Tập 2
Hãy chỉ ra các cặp tam giác đồng dạng trong hình 47.
Lý thuyết các trường hợp đồng dạng của tam giác vuông
1. Áp dụng các trường hợp đồng dạng của tam giác và tam giác vuông