Giải toán 8, giải bài tập toán lớp 8 sgk đầy đủ đại số và hình học Bài 5. Diện tích hình thoi

Bài 34 trang 128 SGK Toán 8 tập 1


Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật . Vì sao tứ giác này là một hình thoi?

Đề bài

Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật . Vì sao tứ giác này là một hình thoi? So sánh diện tích hình thoi và diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa độ dài cạnh ấy.

- Diện tích hình chữ nhật có kích thước hai cạnh \(a,b\) là \(S=a.b\).

- Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.

\(S=\dfrac{1}{2}{d_1}.{d_2}\)

Lời giải chi tiết

Vẽ hình chữ nhật \(ABCD\). \(M, N, P, Q.\) lần lượt là trung điểm các cạnh AD,AB,BC,CD

Vẽ tứ giác \(MNPQ\)

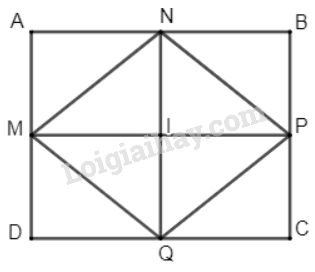
Ta có:

\(MN\) là đường trung bình của tam giác \(ABD\) nên \(MN = \dfrac{1}{2}BD\) (tính chất)

\(PQ\) là đường trung bình của tam giác \(CBD\) nên \(PQ = \dfrac{1}{2}BD\) (tính chất)

\(NP\) là đường trung bình của tam giác \(ABC\) nên \(NP = \dfrac{1}{2}AC\) (tính chất)

\(MQ\) là đường trung bình của tam giác \(ADC\) nên \(MQ = \dfrac{1}{2}AC\) (tính chất)

Mà ABCD là hình chữ nhật nên \(AC = BD\) (tính chất hình chữ nhật) nên suy ra \(MN = PQ = NP = MQ.\)

\(\Rightarrow MNPQ\) là hình thoi (dấu hiệu nhận biết hình thoi)

Ta có: \(∆AMN = ∆INM , ∆BPN = ∆NIP, \)\(\,∆PCQ = ∆IQP, ∆DMQ = ∆IQM\)

\( \Rightarrow {S_{AMN}} = {S_{INM}},{S_{BPN}} = {S_{NIP}},\)\({S_{PCQ}} = {S_{IQP}},{S_{DMQ}} = {S_{IQM}}\)

Ta có: 

\({S_{MNPQ}} = {S_{MNI}} + {S_{NIP}} + {S_{IQP}} \)\(+ {S_{MQI}}\)

\(\begin{array}{l}
= {S_{AMN}} + {S_{BNP}} + {S_{PCQ}} + {S_{MQD}}\\
= \dfrac{1}{2}{S_{ABC{\rm{D}}}} = \dfrac{1}{2}.AB.AD \\= \dfrac{1}{2}.MP.NQ
\end{array}\)

Vậy \({S_{MNPQ}}=\dfrac{1}{2} MP.NQ\).

Do đó diện tích hình thoi bằng nửa tích hai đường chéo.


Bình chọn:
4.2 trên 176 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua