-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số bậc hai y=ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số bậc hai
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Bài tập ôn chương 4 - Hàm số y=ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài tập ôn chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN – HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2
Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông
Bài 92 trang 121 SBT toán 9 tập 1
Giải bài 92 trang 121 sách bài tập toán 9. Cho tam giác cân ABC, AB = AC = 10cm, BC = 16cm. Trên đường cao AH lấy điểm I sao cho AI = 1/3AH. Vẽ tia Cx song song với AH, Cx cắt tia BI tại D...
Đề bài
Cho tam giác cân \(ABC\), \(AB = AC = 10cm\), \(BC = 16cm\). Trên đường cao \(AH\) lấy điểm \(I\) sao cho \(AI = \displaystyle {1 \over 3}AH.\) Vẽ tia \(Cx\) song song với \(AH\), \(Cx\) cắt tia \(BI\) tại \(D\).
a) Tính các góc của tam giác \(ABC\).
b) Tính diện tích tứ giác \(ABCD\).
Phương pháp giải - Xem chi tiết
a) Áp dụng tỉ số lượng giác của góc nhọn và định lí Py-ta-go vào các tam giác vuông.
b) Áp dụng định lí Py-ta-go và kiến thức về đường trung bình của tam giác.
Lời giải chi tiết
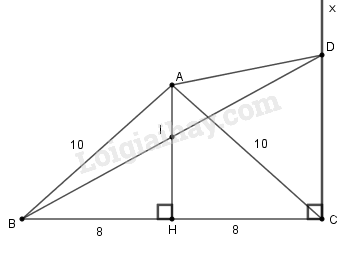
a) Vì tam giác ABC cân tại A có \(AH \bot BC\) nên AH cũng là đường trung tuyến, suy ra: \(HB = HC =\displaystyle {{BC} \over 2} = 8\,(cm)\)
Trong tam giác vuông \(ABH\), ta có:
\(\cos \widehat B = \displaystyle {{HB} \over {AB}} = {8 \over {10}} = 0,8\)
Suy ra: \(\widehat B \approx 36^\circ 52'\)
Vì \(∆ABC\) cân nên \(\widehat B = \widehat C = 36^\circ 52'\)
Ta có: \(\widehat A + \widehat B + \widehat C= 180^\circ \) (tổng 3 góc trong tam giác ABC)
\(\widehat A = 180^\circ - (\widehat B + \widehat C) \)\(= 180^\circ - (36^\circ 52' + 36^\circ 52') = 106^\circ 16'\)
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABH, ta có:
\(\eqalign{
A{B^2} = A{H^2} + B{H^2} \cr
\Rightarrow A{H^2} = A{B^2} - B{H^2}\cr = {10^2} - {8^2} = 36 \cr} \)
Suy ra: \(AH = 6 (cm)\)
Ta có: \(AI = \displaystyle {1 \over 3}.AH = {1 \over 3}.6 = 2\,(cm)\)
Suy ra: \(IH = AH - AI = 6 - 2 = 4 (cm)\)
Vì \(IH \bot BC\) và \(DC \bot BC\) nên \(IH // DC\) (1)
Mặt khác: \(BH = HC\) (cmt) (2)
Từ (1) và (2) ta có \(IH\) là đường trung bình của tam giác \(BCD\).
Suy ra: \(IH =\displaystyle {1 \over 2}CD\) hay \(CD = 2.IH\)\( = 2.4 = 8 (cm)\)
Ta có:
\({S_{ABH}} = \displaystyle {1 \over 2}AH.BH = {1 \over 2}.6.8\)\( = 24\,\,\left( {c{m^2}} \right)\)
Vì \(AH//DC\) nên AHCD là hình thang và \(AH\bot HC\) nên HC là chiều cao của hình thang AHCD. Từ đó:
\({S_{AHCD}} = \displaystyle {{AH + CD} \over 2}.HC = {{6 + 8} \over 2}.8\)\( = 56\,\left( {c{m^2}} \right)\)
Vậy \({S_{ABCD}} = S{ _{ABH}} + {S_{AHCD}} = 24 + 56\)\( = 80\,\) (cm2)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 93 trang 121 SBT toán 9 tập 1
- Bài 94 trang 122 SBT toán 9 tập 1
- Bài 95 trang 122 SBT toán 9 tập 1
- Bài 96 trang 112 SBT toán 9 tập 1
- Bài 97 trang 122 SBT toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
