-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số bậc hai y=ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số bậc hai
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Bài tập ôn chương 4 - Hàm số y=ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài tập ôn chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN – HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2
Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông
Bài 90 trang 121 SBT toán 9 tập 1
Giải bài 90 trang 121 sách bài tập toán 9. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. a) Tính BC, góc B, góc C; b) Phân giác của góc A cắt BC tại D. Tính BD, CD...
Đề bài
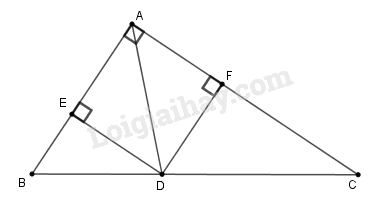
Cho tam giác \(ABC\) vuông tại \(A\), \(AB = 6cm\), \(AC = 8cm.\)
a) Tính \(BC,\widehat B,\widehat C\);
b) Phân giác của góc \(A\) cắt \(BC\) tại \(D\). Tính \(BD, CD\).
c) Từ \(D\) kẻ \(DE\) và \(DF\) lần lượt vuông góc với \(AB\) và \(AC\). Tứ giác \(AEDF\) là hình gì? Tính chu vi và diện tích của tứ giác \(AEDF\).
Phương pháp giải - Xem chi tiết
a) Áp dụng định lí Py-ta-go và tỉ số lượng giác.
b) Vận dụng tính chất đường phân giác tìm độ dài cạnh BD.
c) Áp dụng dấu hiệu nhận biết các hình tứ giác đã học.
Tính chu vi và diện tích của tứ giác.
Lời giải chi tiết
a) Áp dụng định lí Pi-ta-go vào tam giác vuông \(ABC\), ta có:
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} \cr
& = 36 + 64 = 100\,(cm) \cr} \)
Suy ra: \(BC = \sqrt {100} = 10\,(cm)\)
Xét tam giác vuông ABC, theo định nghĩa tỉ số lượng giác của góc nhọn, ta có: \(\sin C =\displaystyle {{AB} \over {AC}} = {6 \over {10}} = 0,6\)
Suy ra: \(\widehat C = 36^\circ 52'\)
Ta có: \(\widehat B + \widehat C = 90^\circ \) (vì tam giác ABC vuông tại A)
\( \Rightarrow \widehat B = 90^\circ - \widehat C = 90^\circ - 36^\circ 52'\)\( = 53^\circ 8'\)
b) Vì AD là đường phân giác của tam giác ABC, nên:
\(\displaystyle {{BD} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác)
Suy ra: \(\displaystyle {{BD} \over {BD + DC}} = {{AB} \over {AB + AC}}\)
\(\Rightarrow \displaystyle {{BD} \over {BC}} = {{AB} \over {AB + AC}}\)
Suy ra: \(BD = \displaystyle {{BC.AB} \over {AB+AC}} = {\displaystyle {10.6} \over {6+8}} = {{30} \over 7}\,(cm)\)
\(DC=BC-BD\)\(=10-\dfrac{30}{7}\)\(=\dfrac{40}{7}\)
c) Ta có: \(\widehat A = \widehat {AED} = \widehat {AFD} = {90^0}\)
Suy ra tứ giác \(AEDF\) có ba góc vuông nên hình đó là hình chữ nhật.
Mặt khác, \(D\) nằm trên tia phân giác của góc \(A\) nên \(DE=DF\) (tính chất tia phân giác của 1 góc)
Vậy tứ giác \(AEDF\) là hình vuông.
Vì \(DE ⊥ AB, AC ⊥ AB\) nên \(DE // AC\)
Theo định lí Ta-lét trong tam giác BAC, ta có:
\(\begin{array}{l}
\dfrac{{CD}}{{BC}} = \dfrac{{AE}}{{AB}}\\
\Rightarrow AE = \dfrac{{CD.AB}}{{BC}} = \dfrac{{\dfrac{{40}}{7}.6}}{{10}} = \dfrac{{24}}{7}
\end{array}\)
Chu vi tứ giác \(AEDF\) bằng: \(4AE = 4.\displaystyle {{24} \over 7} = {{96} \over 7}\,(cm)\)
Diện tích tứ giác \(AEDF\) bằng: \(A{E^2} = \displaystyle {\left( {{{24} \over 7}} \right)^2} = {{576} \over {49}}\,\left( {c{m^2}} \right)\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 91 trang 121 SBT toán 9 tập 1
- Bài 92 trang 121 SBT toán 9 tập 1
- Bài 93 trang 121 SBT toán 9 tập 1
- Bài 94 trang 122 SBT toán 9 tập 1
- Bài 95 trang 122 SBT toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
