Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông

Bài 89 trang 121 SBT toán 9 tập 1


Giải bài 89 trang 121 sách bài tập toán 9. Cho hình thang với đáy nhỏ là 15cm, hai cạnh bên bằng nhau và bằng 25cm; góc tù bằng 120 độ. Tính chu vi và diện tích của hình thang đó...

Đề bài

Cho hình thang với đáy nhỏ là \(15cm\), hai cạnh bên bằng nhau và bằng \(25cm\), góc tù bằng \(120^\circ \). Tính chu vi và diện tích của hình thang đó.

Phương pháp giải - Xem chi tiết

- Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.

- Chu vi hình thang bằng tổng độ dài các cạnh bao quanh của hình đó.

- Diện tích hình thang bằng đáy lớn cộng đáy bé (cùng đơn vị đo) chia 2 rồi nhân với chiều cao.

Lời giải chi tiết

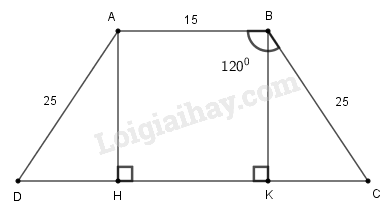
Giả sử hình thang \(ABCD\) có đáy nhỏ \(AB = 15cm\), cạnh bên \(AD = BC \)\(=25cm\), \(\widehat {ABC} = \widehat {BAD} = 120^\circ \).

Kẻ \(AH \bot CD,BK \bot CD\)

Ta có: \(AB//HK\) và \(AH//BK\) (cùng vuông với CD) nên \(ABKH\) là hình bình hành.

Suy ra: \(HK=AB  =15 (cm)\) và \(AH=BK\) 

Vì AB//CD nên \(\widehat {ADC} + \widehat {DAB} = 180^\circ \) (hai góc trong cùng phía)

Suy ra:

\(\widehat {ADC} = 180^\circ  - \widehat {DAB} = 180^\circ  - 120^\circ\)\(  = 60^\circ \)

Trong tam giác vuông \(ADH\), ta có:

\(\eqalign{
& DH = AD.\cos \widehat {ADC} \cr 
& = 25.\cos 60^\circ = 12,5\,(cm) \cr} \)

\(\eqalign{
& AH = AD.\sin \widehat {ADC} \cr 
& = 25.\sin 60^\circ = {{25\sqrt 3 } \over 2}(cm) \cr} \)

Ta có: \(AH=BK\) (cmt) và \(AD=BC\) (gt) nên hai tam giác vuông \(∆ADH=∆BCK\) (cạnh huyền - cạnh góc vuông)

Suy ra: \( CK =DH= 12,5 (cm)\)

Ta có: \(CD=CK + KH + HD\)\(=12,5 + 15 + 12,5=40cm\)

Chu vi hình thang \(ABCD\) là:

\(AB + BC + CD + DA \)

\(= 15 + 25 + 40 + 25\)

\( = 105 (cm)\)

Diện tích hình thang \(ABCD\) là:

\(\eqalign{
& {S_{ABCD}} = {{AB + CD} \over 2}.AH \cr 
& = {{15 + 40} \over 2}.{{25\sqrt 3 } \over 2} \approx 595,392\,\,\left( {c{m^2}} \right) \cr} \)

Loigiaihay.com


Bình chọn:
4.7 trên 20 phiếu
Bài tiếp theo
  • Bài 90 trang 121 SBT toán 9 tập 1

    Giải bài 90 trang 121 sách bài tập toán 9. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. a) Tính BC, góc B, góc C; b) Phân giác của góc A cắt BC tại D. Tính BD, CD...

  • Bài 91 trang 121 SBT toán 9 tập 1

    Giải bài 91 trang 121 sách bài tập toán 9. Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a...

  • Bài 92 trang 121 SBT toán 9 tập 1

    Giải bài 92 trang 121 sách bài tập toán 9. Cho tam giác cân ABC, AB = AC = 10cm, BC = 16cm. Trên đường cao AH lấy điểm I sao cho AI = 1/3AH. Vẽ tia Cx song song với AH, Cx cắt tia BI tại D...

  • Bài 93 trang 121 SBT toán 9 tập 1

    Giải bài 93 trang 121 sách bài tập toán 9. Cho tam giác ABC. Biết : AB = 21cm, AC = 28cm, BC = 35cm. a) Chứng minh tam giác ABC vuông. b) Tính sinB, sinC...

  • Bài 94 trang 122 SBT toán 9 tập 1

    Giải bài 94 trang 122 sách bài tập toán 9. Cho hình thang ABCD. Biết hai đáy AB = a và CD = 2a, cạnh bên AD = a, widehat A = 90 độ. a) Chứng minh tan C = 1...

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store