-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số bậc hai y=ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số bậc hai
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Bài tập ôn chương 4 - Hàm số y=ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài tập ôn chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN – HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2
Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông
Bài 84 trang 120 SBT toán 9 tập 1
Giải bài 84 trang 120 sách bài tập toán 9. Tam giác ABC vuông tại A, AB = a, AC = 3a. trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC. a) Chứng minh: ...
Đề bài
Tam giác \(ABC\) vuông tại \(A\), \(AB = a, AC = 3a\). Trên cạnh \(AC\) lấy các điểm \(D, E\) sao cho \(AD = DE = EC.\)
a) Chứng minh: \(\displaystyle {{DE} \over {DB}} = {{DB} \over {DC}}\)
b) Chứng minh \(∆BDE\) đồng dạng \(∆CDB\)
c) Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng hai cách
Cách 1: Sử dụng kết quả ở câu b);
Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác.
Phương pháp giải - Xem chi tiết
- Áp dụng định lí Py-ta-go trong tam giác vuông.
- Các trường hợp bằng nhau của tam giác.
- Sử dụng: Trong tam giác ABC vuông tại A thì \(tan\widehat {ACB} = \displaystyle {{AB} \over {AC}}\)
Lời giải chi tiết
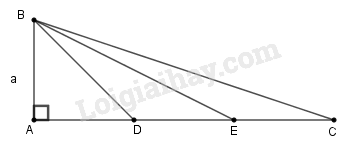
a) Ta có: \(AD = DE = EC = \dfrac{{AC}}{3} = a\)
Áp dụng định lí Pi-ta-go vào tam giác vuông \(ABD\), ta có:
\(B{D^2} = A{D^2} + A{B^2} = {a^2} + {a^2} = 2{a^2}\)
Suy ra: \(BD = a\sqrt 2 \)
Ta có:
\(\eqalign{
& {{DE} \over {DB}} = {a \over {a\sqrt 2 }} = {{\sqrt 2 } \over 2}; \cr
& {{DB} \over {DC}} = {{a\sqrt 2 } \over {2a}} = {{\sqrt 2 } \over 2} \cr} \)
Vậy \(\displaystyle {{DE} \over {DB}} = {{DB} \over {DC}}\)
b) Xét \(∆BDE\) và \(∆CDB\), ta có:
\(\displaystyle {{DE} \over {DB}} = {{DB} \over {DC}}\) (1)
\(\widehat {BDE} = \widehat {BDC}\) (2)
Từ (1) và (2) suy ra \(∆BDE\) đồng dạng \(∆CDB\) (c-g-c).
c) * Cách 1:
Ta có: \(∆BDE\) đồng dạng \(∆CDB\) \(\Rightarrow \widehat {BED} = \widehat {CBD}\)
Mặt khác:
\(\widehat {AEB} + \widehat {BCD} = \widehat {BED} + \widehat {BCD}\)\( = \widehat {CBD} + \widehat {BCD}\) (3)
Trong \(∆BCD\), ta có:
\(\widehat {ADB} = \widehat {CBD} + \widehat {BCD}\) (tính chất góc ngoài) (4)
Lại có: \(\widehat {ADB} = 45^\circ \) (vì ∆ABD vuông cân tại A) (5)
Từ (3), (4) và (5) suy ra: \(\widehat {AEB} + \widehat {BCD} = 45^\circ \)
* Cách 2:
Ta có: \(AE=AD+DE=2a\)
Trong tam giác \( ABE\), ta có:
\(tan\widehat {AEB} = \displaystyle {{AB} \over {AE}} = {a \over {2a}} = {1 \over 2}\)
Suy ra: \(\widehat {AEB} = 26^\circ 34'\)
Trong tam giác vuông \(ABC\), ta có:
\(tan\widehat {ACB} = \displaystyle {{AB} \over {AC}} = {a \over {3a}} = {1 \over 3}\)
Suy ra: \(\widehat {ACB} = 18^\circ 26'\)
Suy ra \(\widehat {AEB} + \widehat {ACB}=26^\circ 34'+18^\circ 26'=45^0\)
Vậy \(\widehat {AEB} + \widehat {ACB} = \widehat {AEB} + \widehat {BCD} = 45^\circ \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 85 trang 120 SBT toán 9 tập 1
- Bài 86 trang 120 SBT toán 9 tập 1
- Bài 87 trang 120 SBT toán 9 tập 1
- Bài 88 trang 121 SBT toán 9 tập 1
- Bài 89 trang 121 SBT toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
