-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI. CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Bài 8. Vị trí tương đối của hai đường tròn (tiếp theo)
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a ≠ 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số bậc hai y=ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số bậc hai
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Bài tập ôn chương 4 - Hàm số y=ax^2 (a ≠ 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - SBT TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, hình quạt tròn
- Bài tập ôn chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN – HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2
Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông
Bài 1.1 phần bài tập bổ sung trang 123 SBT toán 9 tập 1
Giải bài 1.1 phần bài tập bổ sung trang 123 sách bài tập toán 9. Tam giác ABC có góc A bằng 105 độ, góc B bằng 45 độ, BC = 4cm. Tính độ dài các cạnh AB, AC...
Đề bài
Tam giác \(ABC\) có \(\widehat A = 105^\circ \), \(\widehat B = 45^\circ \), \(BC = 4cm\). Tính độ dài các cạnh \(AB, AC.\)
Phương pháp giải - Xem chi tiết
Áp dụng tỉ số giữa cạnh đối và cạnh kề của góc nhọn trong tam giác vuông.
Lời giải chi tiết
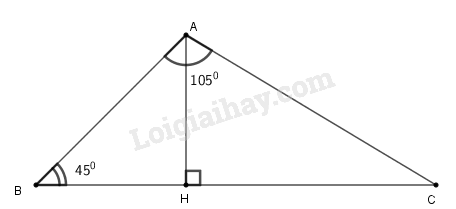
Vẽ đường cao \(AH\). Đặt \(BH = x,\) \(CH = y\) thì do \(H\) nằm giữa \(B\) và \(C\) ( hai góc \(\widehat B,\widehat C\) là góc nhọn) suy ra \(x + y = 4\) (xem hình trên).
Tam giác ABH vuông có \(\widehat B = {45^0}\left( {gt} \right)\) nên ABH là tam giác vuông cân tại H.
Suy ra \(\widehat {BAH} = {45^0} \Rightarrow \widehat {HAC} = \widehat {BAC} - \widehat {BAH}\)
\( = {105^0} - {45^0} = {60^0}\)
Xét tam giác AHC vuông tại H, ta có:
Ta có \( AH = HC.\cot \widehat {HAC}= HC. \cot60^\circ\)\(= \displaystyle {y \over {\sqrt 3 }}\)
Suy ra \(x =BH=AH= \displaystyle {y \over {\sqrt 3 }}\) \( \Rightarrow y = x\sqrt 3 \)
Từ đó \(x + y = 4\)\( \Leftrightarrow x + \sqrt {3}x = 4 \Leftrightarrow x(1 + \sqrt {3}) = 4\) \(\Leftrightarrow x = \displaystyle {4 \over {1 + \sqrt 3 }} \approx 1,46\)
Hay \(BH=AH\approx 1,46\,(cm)\)
Xét tam giác ABH vuông tại H, ta có:
\(AB = \displaystyle {{AH} \over {\sin 45^\circ }} = {{2AH} \over {\sqrt 2 }} \approx 2,06\,(cm)\)
Xét tam giác AHC vuông tại H, ta có:
\(AC = \dfrac{{AH}}{{\cos \widehat {HAC}}} = \dfrac{{AH}}{{\cos {{60}^0}}} \)\(\approx \dfrac{{1,46}}{{\dfrac{1}{2}}} = 2,92\left( {cm} \right)\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.2 phần bài tập bổ sung trang 123 SBT toán 9 tập 1
- Bài 1.3 phần bài tập bổ sung trang 123 SBT toán 9 tập 1
- Bài 1.4 phần bài tập bổ sung trang 123 SBT toán 9 tập 1
- Bài 1.5 phần bài tập bổ sung trang 123 SBT toán 9 tập 1
- Bài 99 trang 122 SBT toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
