-
PHẦN ĐẠI SỐ - TOÁN 8 TẬP 1
-
CHƯƠNG I. PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3. Những hằng đẳng thức đáng nhớ
- Bài 4. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 5. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Ôn tập chương I: Phép nhân và phép chia các đa thức
- Đề kiểm tra 15 phút - Chương 1 - Đại số 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Đại số 8
-
CHƯƠNG II. PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Ôn tập chương II: Phân thức đại số
- Đề kiểm tra 15 phút – Chương 2 – Đại số 8
- Đề kiểm tra 45 phút (1 tiết ) – Chương 2 – Đại số 8
-
-
PHẦN HÌNH HỌC - TOÁN 8 TẬP 1
-
CHƯƠNG I. TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương I: Tứ giác
- Đề kiểm tra 15 phút - Chương 1 - Hình học 8
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 8
-
CHƯƠNG II. ĐA GIÁC, DIỆN TÍCH ĐA GIÁC
- Bài 1. Đa giác. Đa giác đều
- Bài 2. Diện tích hình chữ nhật
- Bài 3. Diện tích tam giác
- Bài 4. Diện tích hình thang
- Bài 5. Diện tích hình thoi
- Bài 6. Diện tích đa giác
- Ôn tập chương II: Đa giác. Diện tích đa giác
- Đề kiểm tra 15 phút - Chương 2 - Hình học 8
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 8
-
-
Đề cương ôn tập học kì 1 toán 8
-
Đề thi học kì 1 mới nhất có lời giải
-
PHẦN ĐẠI SỐ - TOÁN 8 TẬP 2
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
- Bài 1. Mở đầu về phương trình
- Bài 2. Phương trình bậc nhất một ẩn và cách giải
- Bài 3. Phương trình đưa được về dạng ax + b = 0
- Bài 4. Phương trình tích
- Bài 5. Phương trình chứa ẩn ở mẫu
- Bài 6. Giải bài toán bằng cách lập phương trình
- Bài 7. Giải bài toán bằng cách lập phương trình (tiếp)
- Ôn tập chương III: Phương trình bậc nhất một ẩn
-
CHƯƠNG IV. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
-
PHẦN HÌNH HỌC - TOÁN 8 TẬP 2
-
CHƯƠNG III. TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta - let trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta - let
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất
- Bài 6. Trường hợp đồng dạng thứ hai
- Bài 7. Trường hợp đồng dạng thứ ba
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Bài 9. Ứng dụng thực tế của tam giác đồng dạng
- Ôn tập chương III: Tam giác đồng dạng
-
CHƯƠNG IV. HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương IV: Hình lăng trụ đứng. Hình chóp đều
-
ÔN TẬP CUỐI NĂM - TOÁN 8
-
-
Đề thi học kì 2 mới nhất có lời giải
-
Đề cương ôn tập học kì 2
-
Câu hỏi tự luyện Toán 8
-
Tải 30 đề kiểm tra giữa kì 1 Toán 8
-
Tải 30 đề ôn tập kiểm tra học kì 1 Toán 8
-
Tải 30 đề thi học kì 1 của các trường Toán 8
-
Tải 30 đề kiểm tra giữa kì 2 Toán 8
-
Tải 30 đề ôn tập học kì 2 Toán 8
-
Tải 30 đề thi học kì 2 của các trường Toán 8
Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 1 - Hình học 8
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 1 - Hình học 8
Đề bài
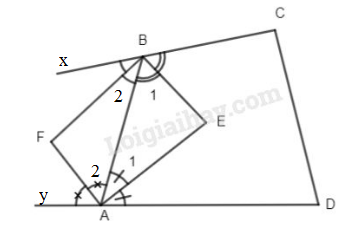
Cho tứ giác ABCD, phân giác trong của góc A và góc B cắt nhau tại E, phân giác ngoài của góc A và góc B cắt nhau tại F.
Chứng minh rằng : \(\widehat {AEB} = {{\widehat C + \widehat D} \over 2}\) và \(\widehat {AFB} = {{\widehat A + \widehat B} \over 2}.\)
Phương pháp giải - Xem chi tiết
Sử dụng: Tổng bốn góc trong tứ giác bằng \(360^0\)
Lời giải chi tiết
Vì BE, AE lần lượt là phân giác góc ABC và góc BAD nên \(\widehat {{B_1}} = \dfrac{{\widehat B}}{2};\widehat {{A_1}} = \dfrac{{\widehat A}}{2}\)
Xét \(\Delta ABE\) có \(\widehat {AEB} = {180^ \circ } - \left( {\widehat {{A_1}} + \widehat {{B_1}}} \right)\)
Suy ra \(\widehat {AEB} = {180^ \circ } - \left( {{{\widehat A} \over 2} + {{\widehat B} \over 2}} \right)\)
\(= {{{{360}^ \circ } - \left( {\widehat A + \widehat B} \right)} \over 2}\)
Lại có \(\widehat A + \widehat B + \widehat C + \widehat D = {360^ \circ }\) (tổng bốn góc trong tứ giác ABCD)
\( \Rightarrow \widehat C + \widehat D =360^0-( \widehat A + \widehat B )\)
\( \Rightarrow \widehat {AEB} = {{\widehat C + \widehat D} \over 2}\)
Ta có: \(\widehat {{B_2}} = \dfrac{{\widehat {xBA}}}{2};\widehat {{A_2}} = \dfrac{{\widehat {yAB}}}{2}\) (tính chất tia phân giác)
Xét \(\Delta ABF\) có \(\widehat {AFB} = {180^ \circ } - \left( {\widehat {{A_2}} + \widehat {{B_2}}} \right)\)
\(\begin{array}{l}
= {180^0} - \left( {\dfrac{{\widehat {xBA}}}{2} + \dfrac{{\widehat {yAB}}}{2}} \right)\\
= \dfrac{{{{360}^0} - \left( {\widehat {xBA} + \widehat {yAB}} \right)}}{2}\\
= \dfrac{{{{360}^0} - \left( {{{180}^0} - \widehat B + {{180}^0} - \widehat A} \right)}}{2}\\
= \dfrac{{\widehat A + \widehat B}}{2}
\end{array}\)
Vậy \( \widehat {AEB} = {{\widehat C + \widehat D} \over 2}\) và \(\widehat {AFB} = {{\widehat A + \widehat B} \over 2}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 2 - Chương 1 - Hình học 8
- Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Hình học 8
- Bài 5 trang 67 SGK Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
