 Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
 Ôn tập cuối năm – Hình học 9
Ôn tập cuối năm – Hình học 9
Bài 5 trang 142 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho tam giác ABC, trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Dựng đường tròn tâm O ngoại
Đề bài
Cho tam giác ABC, trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Dựng đường tròn tâm O ngoại tiếp tam giác DBC. Gọi H và K lần lượt là trung điểm của BC và BD. Chứng minh OH > OK.
Phương pháp giải - Xem chi tiết
Sử dụng định lí: Dây dài hơn thì gần tâm hơn.
Lời giải chi tiết
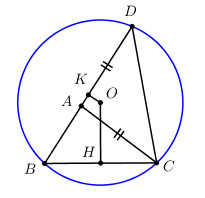
Vì H, K lần lượt là trung điểm của BC và BD nên \(OH \bot BC;\,\,OK \bot BD\) (quan hệ vuông góc giữa đường kính và dây cung).
Áp dụng bất đẳng thức tam giác trong tam giác ABC ta có: \(AB + AC > BC\).
Mà \(AC = AD\,\,\left( {gt} \right) \Rightarrow AB + AD > BC\)
\(\Rightarrow BD > BC \Rightarrow OK < OH\) (dây lớn hơn thì gần tâm hơn).
Vậy \(OH > OK\).
Loigiaihay.com












Danh sách bình luận