Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Ôn tập cuối năm – Hình học 9

Bài 20 trang 143 Tài liệu dạy – học Toán 9 tập 2


Giải bài tập Hai đường tròn (O ; R) và (O’ ; R’) cắt nhau tại A, B sao cho

Đề bài

Hai đường tròn (O ; R) và (O’ ; R’) cắt nhau tại A, B sao cho \(\widehat {OAO'} = {90^o}\) và

OO’ = 2R. Tính theo R diện tích phần chung của hai đường tròn.

Phương pháp giải - Xem chi tiết

Tính diện tích các hình viên phân.

Lời giải chi tiết

 

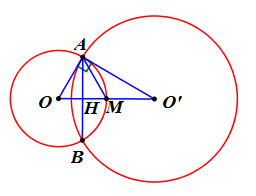
Gọi M là trung điểm của OO’ \( \Rightarrow OM = R \Rightarrow M\) thuộc \(\left( {O;R} \right)\), \(H = AB \cap OO'\).

Xét tam giác vuông OAO’ có: AM là trung tuyến ứng với cạnh huyền \( \Rightarrow AM = \dfrac{1}{2}OO' = OM = O'M\).

\( \Rightarrow OA = OM = AM \Rightarrow \Delta OAM\) đều \( \Rightarrow \widehat {AOM} = {60^0}\).

Xét tam giác vuông OAO’ có: \(\widehat {AOM} + \widehat {AO'M} = {90^0}\) (hai góc nhọn phụ nhau trong tam giác vuông) \( \Rightarrow \widehat {AO'M} = {90^0} - {60^0} = {30^0}\).

Do OO’ là trung trực của AB \( \Rightarrow A\) và B đối xứng nhau qua OO’.

\( \Rightarrow \widehat {AOA'} = {120^0}\) và \(\widehat {AO'B} = {60^0}\)  (tính chất đối xứng).

Xét đường tròn (O) có \({S_{qOAB}} = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{\pi {R^2}.120}}{{360}} = \dfrac{{\pi {R^2}}}{3}\)

Xét tam giác vuông OAH có: \(OH = OA.\cos {60^0} = \dfrac{R}{2};\)

\(\,\,AH = OA.\sin {60^0} = \dfrac{{R\sqrt 3 }}{2} \) \(\Rightarrow AB = R\sqrt 3 \).

\( \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}OH.AB \)\(\,= \dfrac{1}{2}.\dfrac{R}{2}.R\sqrt 3  = \dfrac{{{R^2}\sqrt 3 }}{4}\).

\( \Rightarrow \) Diện tích hình viên phân giới hạn bởi dây cung AB và cung nhỏ AB của đường tròn (O;R) là \({S_1} = {S_{qOAB}} - {S_{\Delta OAB}} = \dfrac{{\pi {R^2}}}{3} - \dfrac{{{R^2}\sqrt 3 }}{4}\).

Xét đường tròn (O’;R’) ta có: \(O'A = OA.\tan {60^0} = R\sqrt 3 \).

\({S_{qO'AB}} = \dfrac{{\pi R{'^2}n}}{{360}} = \dfrac{{\pi .{{\left( {R\sqrt 3 } \right)}^2}.60}}{{360}} \)\(\,= \dfrac{{\pi {R^2}}}{2}\)

Ta có: \(O'H = OO' - OH = 2R - \dfrac{R}{2} = \dfrac{{3R}}{2}\)

\( \Rightarrow {S_{\Delta O'AB}} = \dfrac{1}{2}O'H.AB \)\(\,= \dfrac{1}{2}.\dfrac{{3R}}{2}.R\sqrt 3  = \dfrac{{3{R^2}\sqrt 3 }}{4}\)

\( \Rightarrow \) Diện tích hình viên phân giới hạn bởi dây cung AB và cung nhỏ AB của đường tròn (O’;R’) là \({S_2} = {S_{qO'AB}} - {S_{\Delta O'AB}} = \dfrac{{\pi {R^2}}}{2} - \dfrac{{3{R^2}\sqrt 3 }}{4}\).

Vậy diện tích phần chung của hai đường tròn là

\(S = {S_1} + {S_2}\)\(\, = \dfrac{{\pi {R^2}}}{3} - \dfrac{{{R^2}\sqrt 3 }}{4} + \dfrac{{\pi {R^2}}}{2} - \dfrac{{3{R^2}\sqrt 3 }}{4} \)\(\,= \dfrac{{5\pi {R^2}}}{6} - {R^2}\sqrt 3  = \left( {\dfrac{{5\pi }}{6} - \sqrt 3 } \right){R^2}\)

 Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store