Bài 3 trang 148 Tài liệu dạy – học Toán 9 tập 1

Đề bài

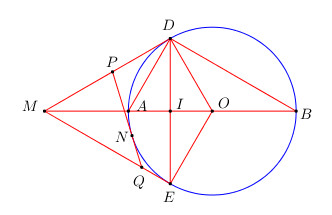
Cho đường tròn (O) đường kính AB = 2R. Vẽ dây DE vuông góc với AO tại I là trung điểm của AO.

a) Chứng minh rằng tam giác ADB vuông. Tính AD, DB theo R.

b) Tiếp tuyến với đường tròn (O) tại D cắt đường thẳng AB tại M. Chứng minh rằng ME là tiếp tuyến của đường tròn (O).

c) Chứng minh rằng : MA.MB = MI.MO.

d) Trên đường tròn (O) lấy điểm N ( N nằm trên nửa mặt phẳng bờ DE chứa điểm A và \(N \ne A\)). Tiếp tuyến với (O) tại N cắt MD ở P và cắt ME ở Q. Trường hợp cho \(\widehat {DME} = {60^o}\), tính theo R chu vi tam giác MPQ.

Lời giải chi tiết

a) Ta có \(\widehat {ADB}\) chắn nửa đường tròn đường kính \(AB \Rightarrow \widehat {ADB} = {90^0}\).

Do đó tam giác \(ADB\) vuông tại \(D\).

Áp dụng hệ thức lượng trong tam giác vuông ADB có: \(A{D^2} = AB.AI = 2R.\dfrac{R}{2} = {R^2} \) \(\Leftrightarrow AD = R\).

Áp dụng định lí Pytago trong tam giác vuông ADB có:

\(D{B^2} = A{B^2} - A{D^2} = {\left( {2R} \right)^2} - {R^2} = 3{R^2}\) \( \Rightarrow DB = R\sqrt 3 \).

b) Xét tam giác vuông ODI và tam giác vuông OEI có:

\(OI\,\,chung\)

\(ID = IE\) (quan hệ vuông góc giữa đường kính và dây cung)

\( \Rightarrow \Delta ODI = \Delta OEI\) (cạnh huyền – cạnh góc vuông)

\( \Rightarrow \angle DOI = \angle EOI\) hay \(\angle MOD = \angle MOE\).

Xét \(\Delta OMD\) và \(\Delta OME\) có :

\(\begin{array}{l}OM\,\,chung;\\\angle MOD = \angle MOE\,\,\left( {cmt} \right)\\OD = OE = R\\ \Rightarrow \Delta OMD = \Delta OME\,\,\left( {c.g.c} \right)\\ \Rightarrow \angle MEO = \angle MDO = {90^0}\end{array}\)

Mà \(OE\) là bán kính của \(\left( O \right) \Rightarrow ME\) là tiếp tuyến của \(\left( O \right)\) tại \(E\).

c) Ta có : \(\angle ADM + \angle ADO = \angle MDO = {90^0}\)

\(OA = OD = AD = R \Rightarrow \Delta OAD\) đều \( \Rightarrow \angle ODA = \angle OAD = {60^0}\)

Xét tam giác vuông ABD có : \(\angle OAD + \angle ABD = {90^0}\)

\( \Rightarrow \angle ADM = \angle ABD\).

Xét \(\Delta ADM\) và \(\Delta DBM\) có :

\(\begin{array}{l}\angle BMD\,\,chung\\\angle ADM = \angle ABD\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ADM \sim \Delta DBM\,\,\left( {g.g} \right) \\\Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MD}}{{MB}} \\\Rightarrow M{D^2} = MA.MB\,\,\left( 1 \right)\end{array}\)

Áp dụng hệ thức lượng trong tam giác vuông ODM có : \(M{D^2} = MI.MO\,\,\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow MA.MB = MI.MO\).

d) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có : \(PD = PN;\,\,QE = QN\)

Ta có : Chu vi tam giác MPQ là:

\({C_{\Delta MPQ}} = MP + MQ + PQ \)\(\,= MP + MQ + PN + QN = MD + ME\).

Mà \(MD = ME\) (tính chất 2 tiếp tuyến cắt nhau). Lại có \(\angle DME = {60^0} \) \(\Rightarrow \Delta MDE\) đều

\( \Rightarrow MD = ME = DE\) \( \Rightarrow {C_{\Delta MPQ}} = 2DE = 4DI\).

Áp dụng hệ thức lượng trong tam giác vuông ABD ta có :

\(D{I^2} = AI.BI = \dfrac{R}{2}.\dfrac{{3R}}{2} = \dfrac{{3{R^2}}}{4}\\ \Rightarrow DI = \dfrac{{R\sqrt 3 }}{2}\).

Vậy khi \(\angle DME = {60^0}\) thì \({C_{\Delta MPQ}} = 4.\dfrac{{R\sqrt 3 }}{2} = 2R\sqrt 3 \).

 Loigiaihay.com