Bài 15 trang 135 SGK Toán 9 tập 2
Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O).Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E.
Đề bài
Tam giác \(ABC\) cân tại \(A\) có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn \((O).\) Tiếp tuyến tại \(B\) và \(C\) của đường tròn lần lượt cắt tia \(AC\) và tia \(AB\) ở \(D\) và \(E.\) Chứng minh:
a) \(BD^2 = AD.CD.\)
b) Tứ giác \(BCDE\) là tứ giác nội tiếp.
c) \(BC\) song song với \(DE.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Trong một đường tròn, góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung thì có số đo bằng nhau.
+) Trong một tứ giác, hai góc có đỉnh liên tiếp cùng nhìn một đoạn thẳng dưới một cặp góc bằng nhau thì là tứ giác nội tiếp.
Lời giải chi tiết
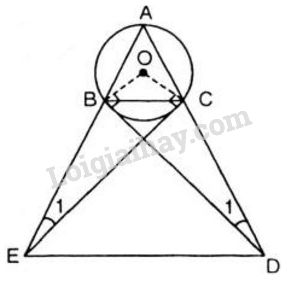
a) Xét \(∆ADB\) v \(∆BDC,\) ta có:
\(\widehat {BA{\rm{D}}} = \widehat {CB{\rm{D}}}\) ( góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BC\)).
\(\widehat {{D_1}}\) góc chung
Vậy \(∆ADB\) đồng dạng \(∆BDC\) (g-g) ⇒ \(\displaystyle {{B{\rm{D}}} \over {C{\rm{D}}}} = {{A{\rm{D}}} \over {B{\rm{D}}}}\) (cặp cạnh tương ứng tỉ lệ)
\(\Rightarrow B{{\rm{D}}^2} = A{\rm{D}}.C{\rm{D}}\) (đpcm)
b) Ta có \(\widehat {A{\rm{E}}C}\) là góc có đỉnh ở bên ngoài \((O)\)
\(\displaystyle \widehat {AEC} = {sđ\overparen{AC}-sđ\overparen{BC}\over 2} = { sđ\overparen{AB}-sđ\overparen{BC}\over 2} = \widehat {ADB}\)
Xét tứ giác \(BCDE\), ta có: \(\widehat {A{\rm{E}}C}\) và \(\widehat {ADB}\) là hai góc kề cạnh ED cùng nhìn đoạn \(BC\) dưới các góc bằng nhau \(\widehat {A{\rm{E}}C} = \widehat {ADB}\) .
Vậy tứ giác \(BCDE\) nội tiếp đường tròn
c) Ta có: \(\widehat {ACB} + \widehat {BC{\rm{D}}} = {180^0}\) (hai góc kề bù).
hay \(\widehat {ABC} + \widehat {BC{\rm{D}}} = {180^0}\) (\(∆ABC\) cân tại \(A\))
\( \Rightarrow \widehat {ABC} = {180^0} - \widehat {BC{\rm{D}}}(1)\)
Vì \(BCDE\) là tứ giác nội tiếp nên
\(\widehat {BE{\rm{D}}} + \widehat {BC{\rm{D}}} = {180^0}\) ( trong tứ giác nội tiếp, 2 góc đối diện có tổng bằng \(180^0\) \( \Rightarrow \widehat {BE{\rm{D}}} = {180^0} - \widehat {BC{\rm{D}}}(2)\)
So sánh (1) và (2), ta có: \(\widehat {ABC} = \widehat {BE{\rm{D}}}\)
Mà 2 góc này ở vị trí đồng vị
\(\Rightarrow BC // DE\) (đpcm)
Các bài khác cùng chuyên mục













Danh sách bình luận