Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 3. Giải hệ phương trình bằng phương pháp thế

Trả lời câu hỏi 3 Bài 3 trang 15 SGK toán 9 tập 2


Cho hệ phương trình:...

Đề bài

Cho hệ phương trình: 

\(\left( {IV} \right):\left\{ \begin{array}{l}
4x + y = 2\\
8x + 2y = 1
\end{array} \right.\)

Bằng minh họa hình học và phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm. 

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Biến đổi để đưa hai phương trình về dạng của hai đường thẳng song song với nhau.

Từ đó vẽ các đường thẳng để chứng tỏ hệ vô nghiệm.

Lời giải chi tiết

Bằng hình học:

Ta có: 

\(\begin{array}{l}
\left\{ \begin{array}{l}
4x + y = 2\\
8x + 2y = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = - 4x + 2\\
2y = - 8x + 1
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = - 4x + 2\\
y = - 4x + \dfrac{1}{2}
\end{array} \right.
\end{array}\)

Vẽ hai đường thẳng \(y=-4x+2\) và \(y = - 4x + \dfrac{1}{2}\) ta thấy hai đường thẳng này không có điểm chung nên hệ phương trình vô nghiệm.

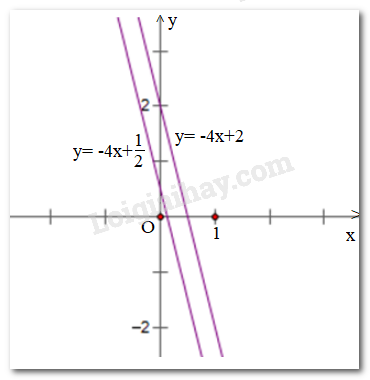
Bằng phương pháp thế:

\(\begin{array}{l}
\left\{ \begin{array}{l}
4x + y = 2\\
8x + 2y = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 2 - 4x\\
8x + 2\left( {2 - 4x} \right) = 1
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = 2 - 4x\\
8x + 4 - 8x = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 2 - 4x\\
4 = 1\left( {vô\,lý} \right)
\end{array} \right.
\end{array}\)

Vậy hệ phương trình đã cho vô nghiệm.

Loigiaihay.com


Bình chọn:
4.3 trên 16 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store