Giải toán 9, giải bài tập toán lớp 9 đầy đủ đại số và hình học Bài 1. Nhắc lại và bổ sung các khái niệm về hàm số

Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Đại số 9


Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Đại số 9

Lựa chọn câu để xem lời giải nhanh hơn

Đề bài

Bài 1. Tìm tập xác định của mỗi hàm số:

a. \(y = {1 \over {\sqrt {x + 2} }}\) 

b. \(y = {1 \over x}\)

Bài 2. Cho hàm số \(y = f\left( x \right) = \sqrt {1 - x} .\) Tính : \(f\left( { - 1} \right);\,f\left( { - 3} \right);\,f\left( 3 \right)\)

Bài 3. Vẽ đồ thị hàm số \(y=-x\)

LG bài 1

Phương pháp giải:

Sử dụng \(\sqrt A \) xác định khi \(A\ge 0\)

\(\dfrac{1}{B}\) xác định khi \(B\ne 0\)

Lời giải chi tiết:

a. Hàm số \(y={1 \over {\sqrt {x + 2} }}\) xác định \( \Leftrightarrow \left\{ {\matrix{   {x + 2 \ge 0}  \cr   {x + 2 \ne 0}  \cr  } } \right. \) 

\(\Leftrightarrow x + 2 > 0 \Leftrightarrow x >  - 2\)

b. Hàm số \(y={1 \over x}\) xác định \( \Leftrightarrow x \ne 0\)

LG bài 2

Phương pháp giải:

Để tính giá trị \({y_0}\) của hàm số \(y = f\left( x \right)\) tại điểm \({x_0}\) ta thay \(x = {x_0}\) vào \(f\left( x \right)\), ta được \({y_0} = f\left( {{x_0}} \right)\).

Lời giải chi tiết:

Vì \(\sqrt {1 - x} \) xác định \( \Leftrightarrow 1 - x \ge 0 \Leftrightarrow x \le 1\) 

Vậy \(f(3)\) không tồn tại (do \(x=3\) không thỏa mãn điều kiện xác định)

Ta có: \(\eqalign{  & f\left( { - 1} \right) = \sqrt {1 - \left( { - 1} \right)}  = \sqrt 2   \cr  & f\left( { - 3} \right) = \sqrt {1 - \left( { - 3} \right)}  = \sqrt 4  = 2 \cr} \)

LG bài 3

Phương pháp giải:

Cách vẽ đồ thị của hàm số \(y = ax + b (a ≠ 0).\)

- Chọn điểm \(P(0; b)\) (trên trục \(Oy\)). 

- Chọn điểm \(Q\left( { - \dfrac{b}{a};0} \right)\) (trên trục \(Ox\)).

- Kẻ đường thẳng \(PQ\) ta được đồ thị của hàm số \(y=ax+b.\)

Lời giải chi tiết:

Bảng giá trị : 

       x

       0                 1

       y

       0                -1

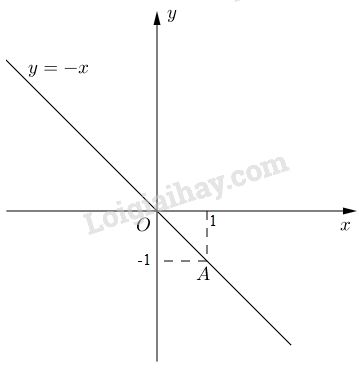
Đồ thị của hàm số \(y = -x\) là đường thẳng qua hai điểm \(O(0; 0)\) và \(A(1; -1)\).

Loigiaihay.com


Bình chọn:
4.4 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com. , cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua